【背景】
矩阵乘法是线性代数中最常见的问题之一,它不仅在数值计算中具有广泛的应用,还是现代机器学习技术中必不可少的基石。
【定义】
\( 设A、B是两个n \times n 矩阵, 他们的乘积AB同样是一个n\times n 矩阵\)即:
\(A_{n\times n} B_{n \times n} = C_{n \times n}\)
\( A和B的乘积矩阵C中各元素C_{ij}定义为:\)\(\begin{align}C_{ij} = \sum_{k=1}^n A_{ik}B_{kj}\end{align}\)
【分析】
若按照上述提及的公式一次对矩阵A、B进行乘积运算。计算C中每一个元素\(C_{ij}\) 需做n次乘法和n-1次加法运算,因此,欲计算出C中每一个元素的时间复杂度为\(O(n^3)\)
其源码如下:
def traditional(matrix1, matrix2): matrix3 = [] for i in range(0, len(matrix1)): temp = [] for j in range(0, len(matrix2)): t = 0 for k in range(0, len(matrix1)): t += matrix1[i][k] * matrix2[k][j] temp.append(t) matrix3.append(temp) return matrix3
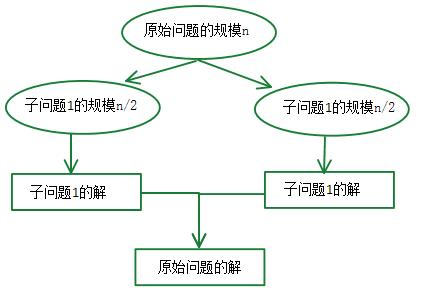
【算法引出-分治法】
根据n阶(此处为了方便叙述,我们假设n是2的幂)矩阵的相关特性,我们可以将每一块矩阵都分为4个大小相等的子矩阵,每一个子矩阵都是n/2×n/2的方阵。于是我们将方程C= AB重写为下述形式:
\(\begin{align}\begin{bmatrix}C_{11} & C_{12} \\ C_{21} & C_{22}\end{bmatrix} = \begin{bmatrix}A_{11} & A_{12} \\ A_{21} & A_{22}\end{bmatrix} \begin{bmatrix}B_{11} & B_{12} \\ B_{21} & B_{22}\end{bmatrix}\end{align}\)
由此可得:
\( \begin{align}&C_{11} = A_{11}B_{11} + A_{12}B_{21} \\&C_{12} = A_{11}B_{12} + A_{12}B_{22}\\&C_{21} = A_{21}B_{11} + A_{22}B_{21}\\&C_{22} = A_{21}B_{12} + A_{22}B_{22}\end{align}\)
其分治递推式如下:
\(\begin{align}T(n) = \begin{cases} O(1) & n =2 \\ 8T(n/2) + O(n^2) & n >2\end{cases}\end{align}\)
利用扩展递归求解得出:
\( T(n) = O(n^3)\)
初次分治,得出的结果与传统公式求解的时间复杂度并没有改变,即这样的分治是徒劳的。
【Strassen矩阵乘法-分治、剪枝】
Strassen算法的核心思想是令递归树稍微不那么茂盛一点儿, 即只递归进行7次而不是8次n/2×n/2 矩阵的乘法。减少一次矩阵乘法带来的代价可能是额外几次n/2×n/2矩阵的加法,但只是常数次 。
算法描述如下:
先按照先前的分治思想中矩阵分解的方法将A,B,C进行分解
创建如下7个\( n/2 \times n/2\)的矩阵\(M_1, M_2,M_3,\dots, M_7\):
\(\begin{align}&M_1 = A_{11}(B_12 – B_{22}) \\ &M_2 = (A_{11} + A_{12})B_{22} \\& M_3 = (A_{21} + A_{22})B_{11} \\& M_4 = A_{22}(B_{21} – B_{11})\\ &M_5 = (A_{11} + A_{22})(B_{11}+B_{22}) \\ & M_6=(A_{12} – A_{22})(B_{21}+B_{22})\\&M_7 = (A_{11} -A_{21})(B_{11} + B_{12})\end{align}\)
做完这7次乘法后,再做若干次加减法就可以得到\(C_{11},C_{12}, C_{21}, C_{22}\),他们的计算公式如下:
\(\begin{align}&C_{11} = M_5 + M_4 – M_2 + M_6 \\ &C_{12} = M_1 + M2 \\ &C_{21} = M3+M4\\&C_{22} = M_5+M_1-M_3-M_7\end{align}\)
其分治递推式如下:
\(\begin{align} T(n) = \begin{cases} O(1) & n =2 \\ 7T(n/2) + O(n^2) & n > 2\end{cases}\end{align}\)
求出:
\( T(n) = O(n^{log7} )\approx O(n^{2.81})\)
其Python源代码如下:
# -*- coding:utf-8 -*- def mergeMatrix(A11, A12, A13, A14): n = len(A11) for i in range(0, n): A11[i].extend(A12[i]) A13[i].extend(A14[i]) for i in range(0,n): A11.append(A13[i]) return A11 def division(matrix): A11 = [] A12 = [] A21 = [] A22 = [] half_size = int(len(matrix) / 2) for i in range(0, half_size): A11.append(matrix[i][:half_size]) A12.append(matrix[i][half_size:]) for j in range(half_size, len(matrix)): A21.append(matrix[j][:half_size]) A22.append(matrix[j][half_size:]) return A11, A12, A21, A22 class Strassen: def add(self, m1, m2, size): matrix = [] for i in range(0, size): temp = [] for j in range(0, size): temp.append(m1[i][j] + m2[i][j]) matrix.append(temp) return matrix def sub(self, m1, m2, size): matrix = [] for i in range(0, size): temp = [] for j in range(0, size): temp.append(m1[i][j] - m2[i][j]) matrix.append(temp) return matrix def multiply(self, m1, m2, size): if(size == 1): return [[m1[0][0] * m2[0][0]]] A11, A12, A21, A22 = division(m1) B11, B12, B21, B22 = division(m2) size = int(size / 2) #calculate M1 = A11(B12 - B22) m1 = self.multiply(A11, self.sub(B12, B22, size), size) #calculate M2 = (A11 + A12)B22 m2 = self.multiply(self.add(A11, A12, size), B22, size) #calculate M3 = (A21 + A22)B11 m3 = self.multiply(self.add(A21, A22, size), B11, size) #calculate M4 = A22(B21 - B11) m4 = self.multiply(A22, self.sub(B21, B11,size), size) #calculate M5 = (A11 + A22)(B11 + B22) m5 = self.multiply(self.add(A11, A22, size), self.add(B11, B22, size), size) #calculate M6 = (A12 - A22)(B21 + B22) m6 = self.multiply(self.sub(A12, A22, size), self.add(B21, B22, size), size) #calculate M7 = (A11 - A21)(B11 + B12) m7 = self.multiply(self.sub(A11, A21, size), self.add(B11, B12, size), size) #calculate C11 = M5 + M4 - M2 + M6 C11 = self.add(self.sub(self.add(m5, m4, size), m2, size), m6, size) #calculate C12 = M1 + M2 C12 = self.add(m1, m2, size) #calculate C21 = M3 + M4 C21 = self.add(m3, m4, size) #calculate C22 = M5 + M1 - M3 -M7 C22 = self.sub(self.sub(self.add(m5,m1,size), m3,size), m7,size) return mergeMatrix(C11, C12, C21, C22) s = Strassen() #print(s.sub([[1,2],[3,4]],[[1,2],[3,4]])) matrixA = [ [1, 1, 1, 1], [1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4] ] matrixB = [ [1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4] ] print(s.multiply(matrixA, matrixB, 4))
【总结】
-
在此问题中,相对于传统算法的复杂度\(O(n^3)\),使用分治+剪枝的Strassen算法的表现\(O(n^{2.81})\)更胜一筹。因此我们知道,在具有某些可以分治处理性质的问题中,也可以多利用分治法思想对问题进行求解。
-
对矩阵乘法问题的研究中,Hopcroft和Kerr已证明,要计算2个2×2 矩阵的乘积,7次乘法是必要的。因此,要想进一步改进矩阵乘法的时间复杂性,就不能再基于计算2×2矩阵的7次乘法这样的方法了。或许应当研究3×3 或5×5矩阵的更好算法。
-
在Strassen之后又有许多算法改进了矩阵乘法的计算时间 复杂性。目前最好的计算时间上界是 \(O(n^{2.376})\)。
-
到目前为止仍无法确切知道矩阵乘法的时间复杂性,关于这一研究课题还有许多工作可做。
【参考文献】
-
王红梅,胡明.《算法设计与分析》[M].清华大学出版社
-
王晓东.《算法设计与分析(第五版)》[M].电子工业出版社
[…] Strassen矩阵乘法(分治、剪枝)[附Python源码] […]
[…] 2、分治法 20190304 20190304 20190304 […]