一、网络的基本表征量

网络的基本表征量可分为以下三类：

1.基本变量：电压： $u (t)$ 、电流： $i (t)$ 、电荷： $q (t)$ 、磁链 $Ψ (t)$ 。

$u = R i$ 表明：电压电流间存在通路（电阻不能为无穷大）； $q = C u$ 表明：电压和电荷存在电容； $ψ = L i$ 表明：电流和磁链间存在电感； $i = \frac{d q}{d t}$ 表明： $q$ 和 $i$ 间有不依赖元件产生的关系； $u = \frac{d ψ}{d t}$ 表明：电磁感应定理： $e = N \frac{d ψ}{d t}$ .

2.基本复合量：功率： $P (t) = u (t) i (t)$ 和能量： $W (t) = \int_{- \infty}^{+ \infty} p (t) d (t)$

3.高阶基本变量： $u^{(α)}$ 和 $i^{(β)}$ 其中 $α 、 β \neq 0, - 1$

x^{(k)} = \frac{d^{k} x}{d t^{k}}, x^{(- k)} = \int_{- \infty}^{t} \int_{- \infty}^{t_{k}} \dots \int_{- \infty}^{t_{2}} x (τ_{1}) d τ_{1} d (τ_{2}) \dots d τ_{k} (k > 0)

x^{(0)} = x

(正数求导，复数求k次积分)

基本表征量之间存在着与网络元件无关的下述普遍关系

$u (t) = \frac{d Ψ (t)}{d t}, Ψ (t) = u^{(- 1)} = \int_{- \infty}^{t} u (τ) d τ$
$i (t) = \frac{d q (t)}{d t}, q (t) = i^{(- 1)} = \int_{- \infty}^{t} i (τ) d τ$
$p (t) = \frac{d W (t)}{d t} = u (t) i (t), W (t) = \int_{- \infty}^{t} p (τ) d τ = \int_{- \infty}^{t} u (τ) i (τ) d τ$

0. 多口元件和多端元件

0.1 多口元件和多端元件的关系

当流入一个端子的电流恒等于流出另一个端子的电流时，这一对端子成为端口。二端元件 $\Leftrightarrow$ 一口元件

例如：变压器的高压侧和低压侧分别是两个端口。

由此可见，端口元件有偶数个端子。

如果多端元件的端子数为偶数，并且两两能组成端口，则称该多端元件为多口元件。

（一）多端元件和多口元件可以互换吗？

如图所示，元件本身有 $n + 1$ 个端子，由KCL定律，通过端子的电流关系为：

i_{0} = i_{1} + i_{2} + \dots + i_{n}

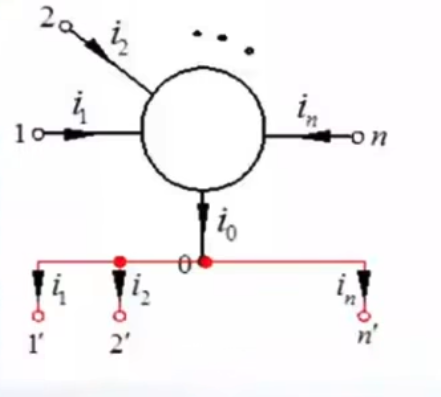
若将 $i_{0}$ 拆分成

i_{1} + i_{2} + \dots + i_{n}

则可得到一个 $n$ 口元件

$n$ 口元件的端口电压、电流列向量表示为：

$u = [u_{1}, u_{2}, \dots, u_{n}]^{T}$ ，

i = [i_{1}, i_{2}, \dots, i_{n}]^{T}

$u, i$ 取关联参考方向

（二）容许信号偶和赋定关系（区分元件）

可能存在元件端口的电压、电流向量随时间的变化或波形成为容许的电压-电流偶，简称容许信号偶，记作 $u (t), i (t)$ .

例如， ${3 \cos ω t, \cos ω t}$ 是3 $Ω$ 电阻的容许信号偶。

${\cos ω t, \cos ω t}$ 不是3 ${Ω}$ 电阻的容许信号偶。

注：容许信号偶也可是 ${u (t), q (t)} 、 {u (t), ψ (t)} 、 {ψ (t), i (t)}$ 。

理论上一个端口元件的容许信号偶有无数个。

元件所有的容许信号偶的集合，称为该元件的赋定关系（本构关系）

当赋定关系只涉及电压电流关系时，称为电压电流关系，记作VCR，或称伏安关系，记作VAR。

赋定关系的范畴大于伏安关系。对二端元件，伏安关系一般指 $u - i$ 平面内的一条曲线，而赋定关系是指所有容许信号偶的集合。

（三）基本二端代数元件（一口元件）

基本二端元件的定义为：

(η, θ) \in {(u, i), (u, q), (i, Ψ), (q, Ψ)}

或 $f (η, θ) = 0$

例如线性电阻元件 $i = i R$ ，电阻元件 $q = C u$ 。

基本二端元件与基本变量的关系如图：

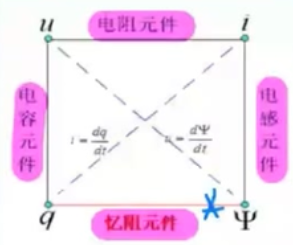
基本二端元件的一般性分类：

$η$ 控元件： $θ = θ (η)$

$θ$ 控元件： $η = η (θ)$

单调元件：元件既是 $η$ 控的，又是 $θ$ 控。

多值元件：元件既不是 $η$ 控的，又不是 $θ$ 控。

关于“控”的理解：

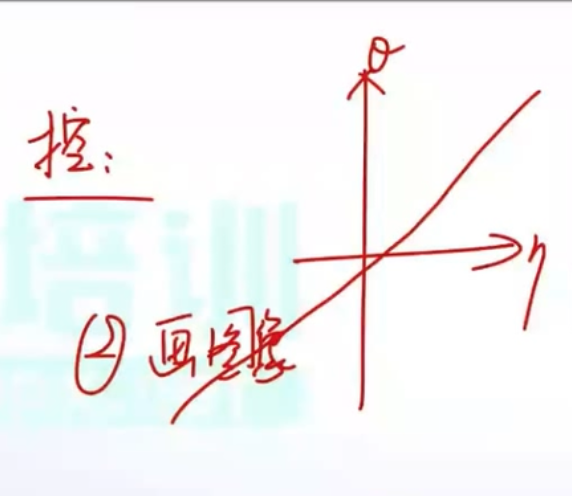
3.1 电阻元件

定义：赋定关系为 $u$ 和 $i$ 之间的代数关系的元件。

R = {(u, i) : f_{R} (u, i) = 0}

电阻元件可分为：

3.1.1 流控电阻

u = g (i)

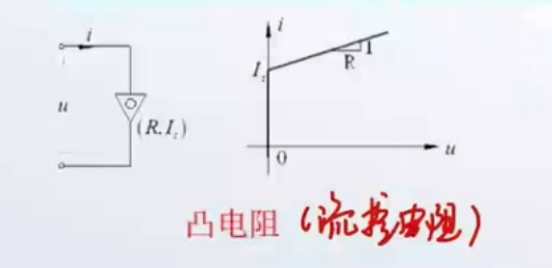
短路是流控电阻

3.1.2 压控电阻

i = r (i)

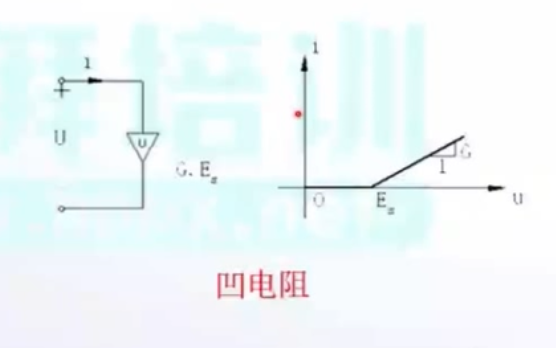
开路是压控电阻

3.1.3 单调电阻

u = g (i), i = r (u)

对任意两组不同容许信号偶 $(u_{1}, i_{1})$ 和 $(u_{2}, i_{2})$ ，恒有：

单增电阻： $(u_{1} - u_{2}) (i_{1} - i_{2}) \geq 0$

严格单调电阻： $(u_{1} - u_{2}) (i_{1} - i_{2}) > 0$

单减电阻： $(u_{1} - u_{2}) (i_{1} - i_{2}) \leq 0$

严格单减电阻： $(u_{1} - u_{2}) (i_{1} - i_{2}) < 0$

3.1.4 仿射电阻

伏安关系 ( $y = k x + b$ )：

$u = R i + U_{s} (U_{s} \neq 0)$ 或 $i = G u + I_{s} (i_{s} \neq 0)$

3.1.5 线性电阻

伏安关系( $y = k x$ ):

$u = R i$ 或 $i = G u$

注意：流控电阻和压控电阻是一般非线性电阻的重要子类，单调电阻是压控电阻和流控电阻的一个子类，仿射电阻是单调电阻的一个特例，而线性电阻又是仿射电阻的一个特例。

3.1.5 多值电阻

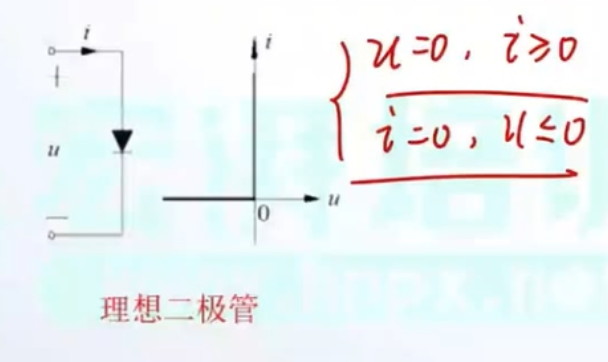
3.2 零口器与非口器（病态元件）

零口器两端电压电流均为零，即：

$u = i = 0$ 或 $u^{2} + i^{2} = 0$

非扣器两端电压电流均为任意值，即：

$u$ 为任意值， $i$ 为任意值，或 $(u - x) (i - y)$ = 0

由外电路来决定。

网络中要出现病态元件，一般是成对出现，才有唯一解。

如图所示，零口器与非口器的串联相当于断路；零口器与非口器的并联相当于短路；零器与若干阻抗的任意串并联组合等同于一个零器；泛器与若干个阻抗的任意串并联组合等同于一个泛器；两对零泛器的星形联接等同于一对（四端）零泛器。（从定义出发进行推理）

由于零口器给出两个方程，因此，只要有一个零口器就会使方程数碧变量数目多一个；同样，由于非扣器不提供方程，因此，只要有一个非口器就会使方程数目碧变量数少一个。只有在零口器与非口器成对出现时，方程数才会与变量数相等。

3.3 独立电源

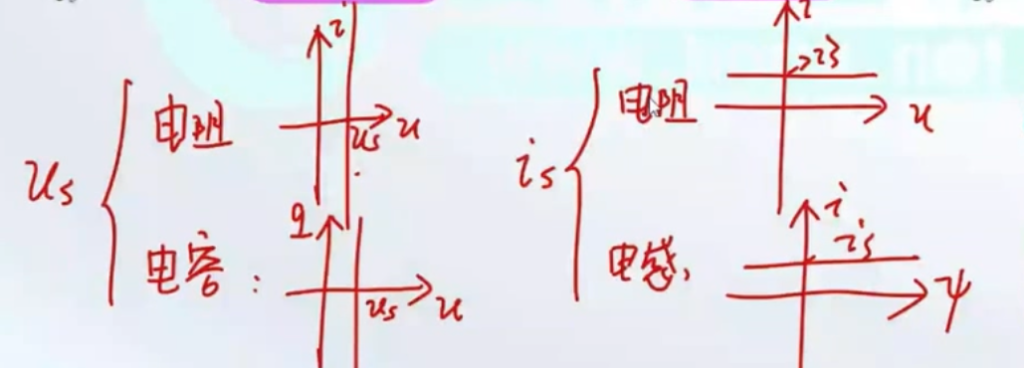
电压源即是流控型元件（视为阻值为0的电阻， $u = u_{s} + 0 i$ ），又是荷控型元件（视为容值为无穷大的电容， $u = u_{s} + \frac{1}{\infty} q$ ）。电流源是压控型元件（视为阻值为无穷大的电阻， $i = i_{s} + \frac{1}{\infty} u$ ），又是链控型元件（视为电感值无穷大的电感， $i = i_{s} + \frac{1}{\infty} ψ$ ）

4.总结

基 本 二 端 代 数 元 件 {\begin{cases} 电 阻 元 件 ： 用 u 和 i 之 间 的 代 数 关 系 表 征 ， 如 u = R i \\ 电 容 元 件 ： 用 u 和 q 之 间 的 代 数 关 系 表 征 ， 如 q = C u \\ 电 感 元 件 ： 用 Ψ 和 i 之 间 的 代 数 关 系 表 征 ， 如 Ψ = L i \\ 忆 阻 元 件 ： 用 Ψ 和 q 之 间 的 代 数 关 系 表 征 Ψ = f (q) \end{cases}

电阻元件不具有记忆特性，属于无记忆（或即时）元件；电容元件、电感元件和忆阻元件都具有记忆特性，属于记忆元件。

（四）高阶二端代数元件

4.1 基本二端代数元件的赋定关系

电阻元件 $f_{R} (u, i) = 0$

电容元件 $f_{C} (u, i^{(- 1)}) = 0$

电感元件 $f_{L} (u^{(- 1)}, i) = 0$

忆阻元件 $f_{M} (u^{(- 1)}, i^{(- 1)}) = 0$

{\begin{cases} f (u^{(α)}, i^{(β)}) = 0, (α, β = 0, - 1) \\ {u^{(α)}, i^{(β)}}, (α, β = 0, - 1) \end{cases}

4.2 高阶二端元件代数元件的赋定关系

赋定关系为 $f (u^{(α)}, i^{(β)}) = 0$ ，称为 $(α, β)$ 元件。

$α$ 和\beta中至少有一个为正时称为高端二端代数元件。 $α$ 和 $β$ 称为端口指数，均为整数。元件的阶数为 $| α - β |_{abs}$ 。

若: $| α - β |_{abs}$ = 0, 1。则对应基本二端代数元件； $| α - β |_{abs} \geq 2$ 则称为高端二端代数元件。

显然，电阻、电容、电感和忆阻元件分别为(0, 0)、(0, -1)、(-1, 0)和(-1, -1)阶元件；电阻和忆阻元件是零阶元件。

注意，在二端元件中的赋定关系中， $(α, β)$ 分别只能取一个值，不能够取多种不同的值。例如： $f (u^{(2)}, i^{(- 1)}) = 0$ 的二端元件是(2, -1)阶元件，但 $f (u^{(2)}, i^{(1)}, i^{(2)}) = 0$ 的二端元件就不是高阶二端元件。

4.2.1 频变负阻元件

（1）D元件

i = D \frac{d^{2}}{d t^{2}}

推导 => $Z (j ω) = \frac{U (j ω)}{I (j ω)} = - \frac{1}{ω^{2} D}$

（2） E元件

u = E \frac{d^{2} i}{d t^{2}}

推导=> $Z (j ω) = \frac{U (j ω)}{I (j ω)} = - ω^{2} E$

(五)代数多口元件的分类

多口元件可以分为代数多口元件和动态多口元件。

代数多口元件可分为基本代数多口元件和高阶和混合代数多口元件。

5.1 基本代数多口元件

n口元件的赋定关系由 $η$ 和 $θ$ 的代数关系表征，满足

F (η, θ) = 0

其中， $(η, θ) \in {(u, i), (u, q), (i, Ψ), (q, Ψ)}$ ， $u, i, q, Ψ$ 分别表示n维端口电压、电流、电荷和磁链的列向量。

5.2 高阶和混合多口元件

高阶和混合代数元件满足赋定关系：

F (η, θ) = 0

【知识体系】电网络理论（二）网络及其元件的基本概念

作者WellLee

一、网络的基本表征量