(一)集总参数电路与分布参数电路
集总参数电路，又叫集中参数电路，目前学术界有两种定义方式：
第一种定义：
如果电路工作频率对应的电磁波的波长 \(\lambda\) 远大于电路本身尺寸\(l \)，则认为电路的各种参数“集中”于一点，元件是一个完整的不可分割的整体。电路中的电压，电流将不是距离的函数，则称该电路为集总参数电路，否则称为分布参数电路；
但是，该定义方式以电磁波波长 \(\lambda\) 作为参考，不适合高压直流输电线路，所以该定义不完备。
第二种定义：
对于多端子设备，如果在任何时刻 \(t\) ，流入任一端子的电流恒等于其它端子流出电流的代数和，且端子之间的电压为单值量，则称该元件为集总参数元件（简称集总元件），否则称为分布参数元件（简称分布元件）
（二）时变与时不变电路
设 \(\{u(t), i(t)\}\) 为某二端元件的任意容许偶，\(T \) 为任意常数。如果\(\{u(t), i(t)\}\) 也是该元件的容许偶，则称该元件为时不变的，否则称为时变的。该定义也可以扩展到\(n\) 端口网络。
例1： 证明电感\(\psi = L(t)i(t)\)为时变一端口元件，其中\(L(t)\) 不随\(u,i\) 变化。
证：设\(\{u_1(t), i_1(t)\}\) 为任意容许偶，\(T\) 为任意实常数
令：\(i_2(t) = i(t-T)\)
则有：\(\psi_1 = L(t)i_1(t), \psi_2 = L(t)i_2(t) = L(t)i_1(t-T)\)
与：\(i_1(t), i_2(t) = i_1(t-T)\) 对应的电压表达式分别如下所示：
\(u_1(t) = \frac{d\psi_1}{dt} = \frac{dL(t)}{dt}i_1(t) = L(t)\frac{di_1(t)}{dt}\)和\(u_2(t) = \frac{d\psi_2}{dt} = \frac{dL(t)}{dt}i_2(t) + L(t)\frac{di_2(t)}{dt} = \frac{dL(t)}{dt}i_1(t-T)+ L(t)\frac{di_1(t-T)}{dt}\)
显然：\(u_2(t) \neq u_1(t-T)\)
所以\(\{u_1(t-T), i_1(t-T)\}\) 不是容许偶
所以该元件为时变一端口元件。
如果\(L(t)\) 为与时间无关的常数 L(t) = L = const
设\({u_1(t), i_1(t)}\) 为其任意容许偶，\(T\) 为任意实常数
令\(i_2(t) = i_1(t-T)\) 则有：\(\psi_1 = Li_1(t), \psi_2 = Li_2(t) = Li_1(t-T)\)
则：\(i_1(t), i_2(t) = i_1(t-T)\) 对应的电压表达式分别如下所示：
\(u_1(t) = \frac{d\psi_1}{dt} = L\frac{di_1(t)}{dt}\)与：\(u_2(t) = \frac{d\psi_2}{dt} = L\frac{di_2(t)}{dt} = L\frac{di_1(t-T)}{dt} = u_1(t-T)\)
所以，\(\{u_1(t-T), i_1(t-T)\}\) 是容许偶，该元件为时不变一端口元件。
由以上例子可以看出，一般\(R, C, L\) 参数不随时间变化时，它们是时不变元件，若其参数是时间函数，则是时变元件。
例2：判断独立电压源\(u(t) = E\sin \omega t\)是否是时不变元件。
证明：设\(\{u_1(t), i_1(t)\}\) 是该元件任意一对容许偶，\(T\) 是任意常数，
则：\(u_1(t-T) = E \sin \omega(t-T)\)
其是一个滞后于电源\(u(t)\) 角度\(\omega T\) 的另一个电压，原电压源不容许有这个电压，所以独立交流电压源是时变元件。
例3：试证明，图示电路为时变一端口，但为非时变（时不变）电路。
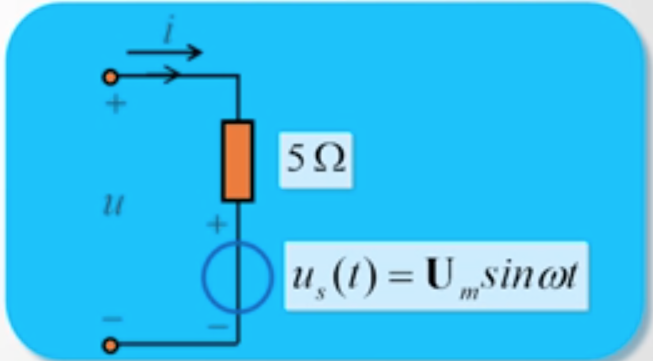
证：（1）由KVL得：端口电压、电流关系
\(u(t) = 5i(t)+U_m \sin \omega t\)设\(\{u_1(t), i_1(t)\}\) 为任意容许偶，
令：\(i_2(t) = i_1(t-T)\)，其中\(T\)为任一实常数
\(u_2(t) = 5i_2(t)+U_m \sin \omega t = 5i_1(t-T)+U_m \sin \omega t \neq u_1(t-T)\)所以，\(\{u_1(t-T), u_2(t-T)\}\)不是容许偶，该网络是时变一端口网络。
（2）由任何一种电路分析方法均可得到，图示电路中任何一个电压或电流响应均可表示为：
\(f(t) = ku_s(t)\)对图示电路\(k\) 为实常数，若激励源\(u_s(t)\)有一个延迟，响应\(f(t)\)也有一个同步的延迟，所以电路是时不变电路。
时变/时不变元件与端口，是讨论端口的\(u\)与\(i\)的函数关系。
时变/时不变电路，是讨论电路中响应跟激励（电源）的函数关系。
电源看成一种电路元件，直流是时不变，交流是时变元件，看成激励源，即使是时变电源，但其所在电路却是是不变的。
由独立源（作为激励可以是时变的）和时不变元件构成的电路称为时不变电路，否则称为时变电路。
（三）线性与非线性
设\(\{u_1, i_1\}\)和\(\{u_2, i_2\}\)为某二端元件的任意两组容许偶，\(\alpha, \beta\) 是任意两个实常数，如果有：\(\{ \alpha u_1 + \beta u_2, \alpha i_1 + \beta i_2\)\}也是该元件的容许偶，则称该元件是线性的，否则称为非线性的。
该定义也可以扩展到多端口网络。
线性和非线性可表述为：齐次性和可加性
齐次性：如果\(\{u_1, i_1\}\)为容许偶\(\{\alpha u_1, \alpha i_1 \}\)也为容许偶，
写成函数关系为：\(f(\alpha x) = \alpha f(x)\)
可加性：如果\( \{ u_1, i_1\}, \{u_2, i_2\}\)为容许偶\(\{u_1 + u_2, i_1 + i_2\}\)也为容许偶。
写成函数关系式为：\(f(x_1 + x_2) = f(x_1) + f(x_2)\)
例1 已知电容元件\(C(t) = C_0 + C_1 \sin \omega t\)，判断该元件的性质。
证：该元件的表达式显含时间\(t\)，所以该元件为时变元件。
\(q(t) = C(t)u(t), i(t) = \frac{d[C(t)u(t)]}{dt}\)设\(\{u_1, i_1\}, \{u_2, i_2\}\)为任意两组容许偶，则有
\(i_1(t) = \frac{d[C(t)u_1(t)]}{dt}, i_2 = \frac{d[C(t)u_2(t)]}{dt}\)设\(\alpha, \beta\)为任意两个实常数，则有：
\(u_3(t) = \alpha u_1(t) + \beta u_2(t)\)。
进一步地：\(i_3(t) = \frac{d[C(t)u_3(t)]}{dt} = \frac{d}{dt}\{C(t)[\alpha u_1(t)+ \beta u_2(t)]\}\)
化简上述：\(=\alpha \frac{d[C(t)u_1(t)]}{dt} + \beta \frac{C(t)u_2(t)}{dt} = \alpha i_1(t) + \beta i_2(t)\)
所以\( \{ \alpha u_1(t) + \beta u_2(t), \alpha i_1(t), \beta i_2(t)\}\) 也是容许偶。
所以该元件为线性时变元件。
例2： 试验证图示电路为非线性一端口，但为线性电路。
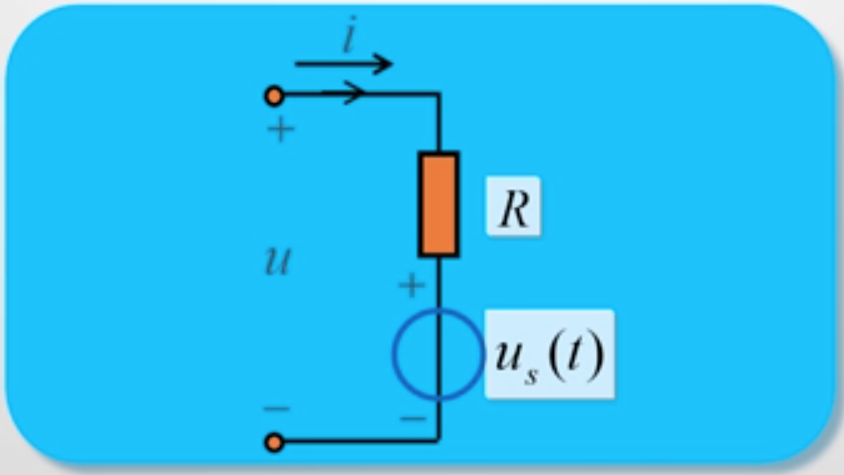
证：（1）由KVL得 \( u(t) = Ri(t) + u_s(t)\)
设\(\{u(t), i(t)\} \)和\(u_2(t), i_2(t)\)是任意两组容许偶。
则：\( u_1(t) = Ri_1(t) + u_s(t), u_2(t) = Ri_2(t) + u_s(t)\)
设\( \alpha,\beta\)是两个任意实常数, \(i_3 = \alpha i_1(t) + \beta i_2(t) \)
则有：\( u_3(t) = Ri_3(t) + u_s(t) = R(\alpha i_1(t) + \beta i_2(t)) + u_s(t) \)
化简得 \( \alpha (i_1(t) + u_s(t)) + \beta (i_2(t) +u_s(t) – (1 – \alpha -\beta) \neq \alpha u_1(t) + \beta u_2(t) \)
所以：\( \{ \alpha u_1(t) + \beta u_2(t), \alpha i_1(t) + \beta i_2(t)\}\)不是容许偶。
所以该元件为非线性一端口元件。
（2） 由任何电路分析方法可得
电路中任何一个电压或电流响应可写成\(f(t) = ku_s(t) \)
对图示电路，\(k\)为实常数，很显然响应 \( f(t) \) 和激励源 \( u_s(t) \) 为线性函数关系，满足齐次性和可加性，所以该电路是线性电路。
讨论线性/非线性原件与端口，是讨论端口的\(u, i \)关系。
讨论线性/非线性电路，是讨论电路中响应与激励（电源）的关系。
电源看做一种电路元件，是非线性元件。看成激励源，即使是激励源，但所在电路却是线性的。
由独立源（作为激励是非线性的）和线性元件构成的电路是线性电路，否则称为非线性电路。
（四）网络的有源性和无源性
严格定义如下：
设\({u_(t), i_(t)}\) 为\(n \)端口网络的任意容许偶，对任意时刻\( t \)，如果网络吸收的能量\( W(t) \geq 0\)，则称该\( n \)端口网络是无源的，否则该\( n \) 端口网络是有源的。
\(w(t) = \int_{-\infty}^t u^{T}(t) i(t) dt > 0, w(t) = \int_{t_0}^{t} u^T(t)i(t) + w_0(t_0) > 0\)无源元件在任何时刻获得的总能量为正，或者说它释放的能量（比如：电容和电感）不超过它过去获得的能量。
有源与无源区分的标志是元件是否能持续地提供电能。
一般来说，参数正常的R,L,C元件均为无源元件，否则为有源元件。
例：对于线性时不变电感\( L \)，其所吸收的能量为：
\( w(t) = \int_{-\infty}^{t} L\frac{di(t)}{dt}i(t)dt = \int_{-\infty}^{t}Li(t)di(t)dt = \frac{1}{2}Li^2(t)\)在该表达式中，只要\( L \geq 0\)，就能保证总能量\( W(t) \geq 0 \)
所以正值的电感是无源元件，负值的电感是有源元件。
例：已知某二端电感元件\(\psi = i^3 – i \)请判断该元件是无源元件还是有源元件
对于该非线性电感元件，假定其吸收的能量为\( w(t) \)，则有：
\(w(t) = \int_{-\infty}^{t}uidt=\int_{-\infty}^{t} (\frac{d\psi}{dt} \cdot i) dt = \int_{-\infty}^{t} (3i^3 – i)di = (\frac{3}{4} i^4 – \frac{1}{2}i^2)|_{i(-\infty)}^{i(t)} \)因为\(i(-\infty) = 0 \)，所以\( w(t) = \frac{3}{4}i^4(t) – \frac{1}{2}i^2(t) \)
当电流\( -\frac{\sqrt{6}}{3} < i < -\frac{\sqrt{6}}{3}\)时，有\( w(t) < 0\)
所以该元件是有源元件。
时不变电阻网络的无源判断
对于线性时不变电阻网络，当且仅当任意的容许偶\(\{u(t), i(t)\} \)和任意时刻\( t\)，网络吸收的功率：
\( p(t) = u^T(t) i(t) \geq 0\)则该电阻网络是无源的。
充分性证明：
电阻网络不存储能量，故有初始储能\(w(t_0) = 0 \)
因为\( p(t) = u^T(t) i(t) \geq 0 \)
则：\( w(t) = w_0(t) + \int_{t_0}^t u^T(\tau) i(\tau) d\tau \geq 0\)
该元件为无源元件。
必要性证明：
假设存在时刻\(t_1 \)，则\( p(t_1) = u^T(t_1)i(t_1) < 0\)
取直流信号\(u(t) = u(t_1), i(t) = i(t_1) \)。
为一组容许信号偶。
则有：\(w(t) = \int_{t_0}^t u^T(t_1)i(t_1)d\tau < 0 \)
则该网络为有源网络，与题干相矛盾，所以若电阻是无源的，则必有任何时刻其吸收功率\( p(t) \geq 0\)
对于一般的元件和网络，判断其有源与无源特性时，需要判断其吸收的能量\(w(t) \)是否一直大于等于0
而对于电阻元件和电阻性网络，判断其有源与无源特性时，可简化为判断功率\(p(t)\)是否大于等于0
例：判断图示电路中受控源控制系统\(\beta \)的取值对二端口网络有源无源性的影响。
解：该电路是一个纯电阻的二端口网络。
首先，列出电路方程
\( u_1 = r_1 i_1, i_2 = \beta i_1 + \frac{1}{r_2}u_2\)。
由方程写出H参数矩阵与Z参数矩阵如下：
\(H = \left[\begin{matrix} r_1 & 0 \\ \beta &\frac{1}{r_2}\end{matrix} \right] \) \( Z = \left[\begin{matrix} r_1 & 0 \\ -\beta r_2& r2 \end{matrix} \right]\)写出该二端口网络吸收的总功率\( p(t)\)表达式，并利用Z矩阵将电压u使用电流i表示：
\(p(t) = \sum_{k=1}^2 u_k i_k = u_1i_1 + u_2 i_2 = i_1r_1i_1 + (i_2 – \beta i_1)r_2i_2 \)得：\([i_1, i2] \left[\begin{matrix} r_1 & -\frac{1}{2}\beta r_2 \\ -\frac{1}{2}\beta r_2&r2\end{matrix} \right] \left[\begin{matrix}i_1 \\ i_2\end{matrix}\right]\)
该矩阵正定，则不管电流\( i_1, i_2\)取何值，都有：
\( p = [i_1, i2] \left[\begin{matrix} r_1 & -\frac{1}{2}\beta r_2 \\ -\frac{1}{2}\beta r_2&r2\end{matrix} \right] \left[\begin{matrix}i_1 \\ i_2\end{matrix}\right] \geq 0\)则该二端口电阻性网络无源的条件是：
\(r_1 \geq 0, \det \left|\begin{matrix} r_1 & -\frac{1}{2}\beta r_2 \\ -\frac{1}{2}\beta r_2&r2\end{matrix}\right| \geq 0\)即：\( \beta \leq 2 \sqrt{\frac{r_1}{r_2}}\)时无源。\( \beta \geq 2 \sqrt{\frac{r_1}{r_2}}\)时有源。