【背景】
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
【源码运行环境】
操作系统:Windows 10
编译环境:Dev C++(基于C99标准)
【动态图解】
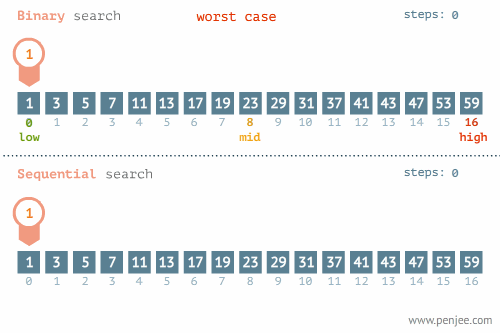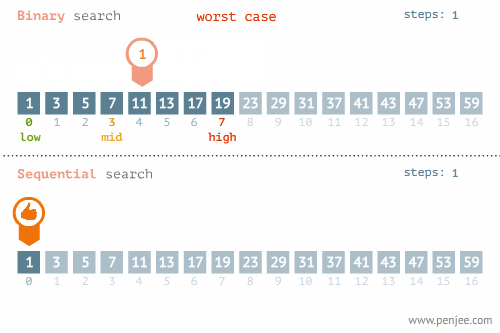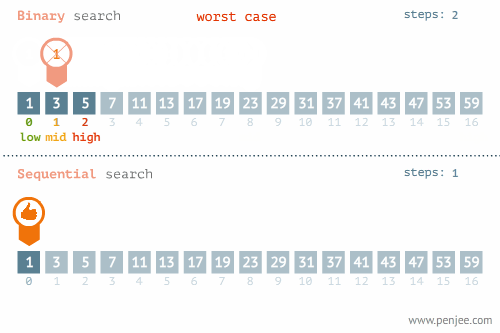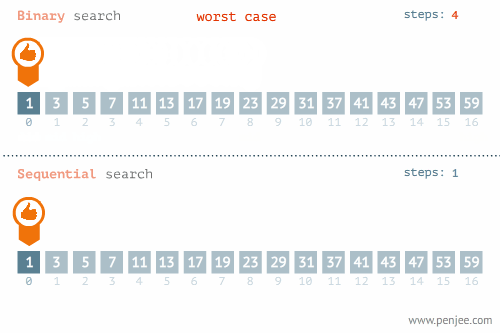
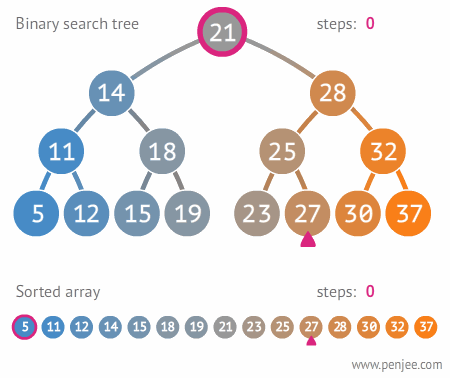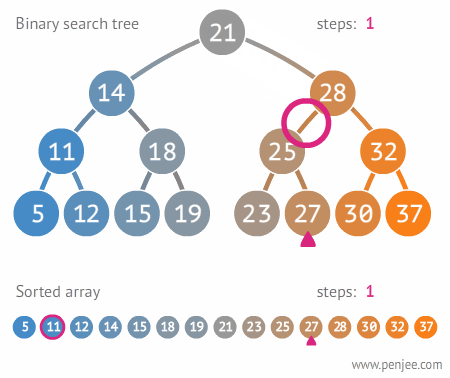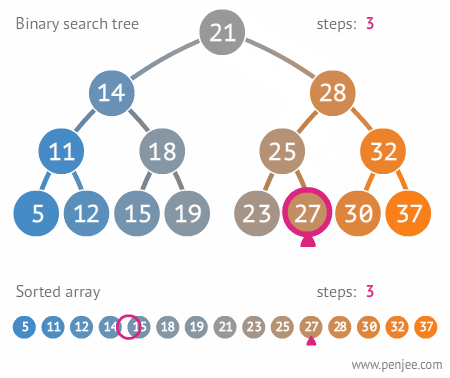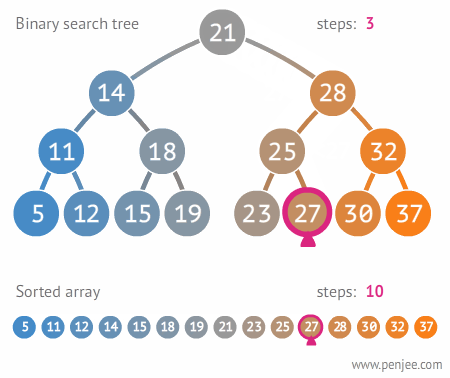
【源码】
递归实现:
/*
*方法名:binary_Search
*作用:折半查找,查找数组中是否存在指定元素,并返回位置
*参数:待查找数组 array; 起始位置 start ; 结束位置 end; 元素 element
*返回值:位置 position
*Author: WellLee
*最后一次修改时间:2018年12月6日 22:18:55
*/
int binary_Search(int array[], int start, int end, int element)
{
int mid;
if(start > end)
{
return -999;
}
mid = (start + end) / 2;
if(element == array[mid])
{
return mid;
}
else if(element >= array[mid])
{
return binary_Search(array,mid+1, end, element);
}
{
return binary_Search(array,start, mid - 1, element);
}
}
非递归实现:
/*
*方法名:Binary_Search
*作用:折半查找,查找数组中是否存在指定元素,并返回位置
*参数:待查找数组 array; 数组长度 length; 元素 element
*返回值:位置 position
*Author: WellLee
*最后一次修改时间:2018年12月6日 22:27:32
*/
int Binary_Search(int array[],int length, int element)
{
int start = 0;
int end = length;
int mid = 0;
while(start <= end)
{
mid = (start + end) / 2;
if(element == array[mid])
{
return mid;
}else if(element > array[mid]){
start = mid + 1;
}else{
end = mid - 1;
}
}
return -999;
}
【分析】
折半查找的平均查找长度(ASL)计算公式如下:
假设表中每个记录的查找概率相等为:\( P_i = \frac{1}{n}\)
\(\begin{align} ASL &= \sum_{i=1}^{n} P_i C_i \\ &= \frac{1}{n} \sum_{i=1}^{h} j \cdot 2^{j-1} \\ &= \frac{n+1}{n} \log_2(n+1) -1 \end{align}\)当n较大时,可近似看做:\(ASL = \log_2(n+1) -1\)
因此,折半查找的时间复杂度为\( O(\log_2 n)\)
【总结】
折半查找的优点是:比较次数少,查找效率高。
其缺点是:对表结构要求高,只能用于顺序存储的有序表。而有序表的构造需要付出较大的时间代价。
因此,折半查找不适用于数据元素经常变动的线性表。
【参考文献】
-
《大话数据结构》.程杰.清华大学出版社
-
《数据结构习题解析与实验指导》.李冬梅,张琪.人民邮电出版社
