【高等数学】函数极值相关问题的一些总结

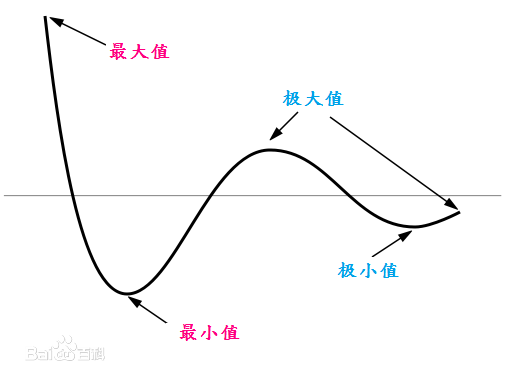
【背景】

我们在高等数学上中学过一元函数求极值，在高等数学下中学了多元函数极值，现将两类问题汇总，做些总结，整合成一个小体系。为做题提供一些帮助。

【知识框体】

极 值 {\begin{cases} 一 元 ： y = f (x) ： {\begin{cases} 1 、 x \in D \\ 2 、 f^{'} (x) {\begin{cases} = 0 & 驻 点 \\ \neq 0 & 极 值 不 存 在 \end{cases} \\ 3 、 判 别 法 ： {\begin{cases} ① 第 一 判 别 法 \\ ② 第 二 判 别 法 \end{cases} \end{cases} \\ 多 元 {\begin{cases} 一 、 无 条 件 极 值 : z = f (x, y) {\begin{cases} 1 、 (x, y) \in D (开 区 间) \\ 2 、 {\begin{cases} \frac{\partial z}{\partial x} = 0 \\ \frac{\partial z}{\partial y} = 0 \end{cases} \Rightarrow {\begin{cases} x = 0 \\ y = 0 \end{cases} (驻 点) \\ 3 、 判 别 法 (x_{0}, y_{0}) 为 驻 点 ： \\ A = f_{x x}^{″} (x_{0}, y_{0}), B = f_{x y}^{″} (x_{0}, y_{0}), C = f_{y y}^{″} (x_{0}, y_{0}) \\ A C - B^{2} {\begin{cases} > 0 \to 是 极 值 点 {\begin{cases} A < 0 & 极 大 点 \\ A > 0 & 极 小 点 \end{cases} \\ < 0 \to 非 极 值 点 \end{cases} \end{cases} \\ 二 、 条 件 极 值 {\begin{cases} 1 、 拉 格 朗 日 乘 数 法 \\ 2 、 定 积 分 法 \end{cases} \end{cases} \end{cases}

【对判别法的一些补充】

1、一元函数极值判别法

①第一判别法 $f^{'} (x_{0}) = 0$

1） ${\begin{cases} x < x_{0} & f^{'} (x) < 0 \\ x > x_{0} & f^{'} (x) > 0 \end{cases} \Rightarrow x_{0} 为极小点$

2) ${\begin{cases} x < x_{0} & f^{'} (x) > 0 \\ x > x_{0} & f^{'} (x) < 0 \end{cases} \Rightarrow x_{0} 为极大点$

②第二判别法

f^{'} (x_{0}) = 0 \to f^{″} (x_{0}) {\begin{cases} > 0 & x_{0} 为 极 小 点 \\ < 0 & x_{0} 为 极 大 点 \end{cases}

2、多元函数极值判别法（针对条件极值）

①拉格朗日乘数法求极值

case 1: $z = f (x, y), 受制于（ S . T ） φ (x, y) = 0$

\begin{aligned} 1 、 令 F (x, y, λ) = f (x, y) + λ φ (x, y) \\ 2 、 求 x, y, λ 的 偏 导 数 \to {\begin{cases} \frac{\partial F}{\partial x} = f_{x}^{'} + λ φ_{x}^{'} = 0 \\ \frac{\partial F}{\partial y} = f_{y}^{'} + λ φ_{y}^{'} = 0 \\ \frac{\partial F}{\partial λ} = φ (x, y) = 0 \end{cases} \Rightarrow {\begin{cases} x = ? \\ y = ? \end{cases} \\ 3 、 将 (x, y) 代 入 1 式 \end{aligned}

case 2 : $u = f (x, y, z), 受制于 (S . T) {\begin{cases} φ (x, y, z) = 0 \\ ψ (x, y, z) = 0 \end{cases}$

\begin{aligned} 1 、 令 F = f + λ φ + u ψ \\ 2 、 求 偏 导 {\begin{cases} F_{x}^{'} = f_{x}^{'} + λ φ_{x}^{'} + u ϕ_{x}^{'} = 0 \\ F_{y}^{'} = f_{y}^{'} + λ φ_{y}^{'} + u ψ_{y}^{'} = 0 \\ F_{z}^{'} = f_{z}^{'} + λ φ_{z}^{'} + u ψ_{z}^{'} = 0 \\ F_{λ}^{'} = φ (x, y, z) = 0 \\ F_{u}^{'} = ψ (x, y, z) = 0 \end{cases} \Rightarrow {\begin{cases} x = ? \\ y = ? \\ z = ? \end{cases} \\ 3 、 将 (x, y, z) 代 入 1 式 \end{aligned}

②定积分法求极值

所谓定积分法求极值，就是利用定积分思想，将多元利用三角函数、参数方程等共计降维度，再用特定工具进行讨论即可，如三角函数的极值范围，参数方程t的取值范围等。

【总结】

本章对试题常见的求极值类型做了总结，并归纳了一些解题技巧，在做题中要充分明确考查的范围并对号入座，这样解题的速度就会得到质的飞跃，当然题量得做够。

【参考文献】

《高等数学》第七版-上册同济大学数学系编
《高等数学》第七版-下册同济大学数学系编

【高等数学】函数极值相关问题的一些总结

作者WellLee

【背景】

【知识框体】

【对判别法的一些补充】

1、一元函数极值判别法

①第一判别法 $f^{'} (x_{0}) = 0$

②第二判别法

2、多元函数极值判别法（针对条件极值）

①拉格朗日乘数法求极值

②定积分法求极值

【总结】

【参考文献】

作者 WellLee

相关文章

【知识体系】电网络理论（三）电网络的基本性质

【知识体系】电网络理论（二）网络及其元件的基本概念

【知识体系】电网络理论（一）综述

发表回复取消回复

You missed

【知识体系】电网络理论（三）电网络的基本性质

【知识体系】电网络理论（二）网络及其元件的基本概念

【知识体系】电网络理论（一）综述

【实验室运维】Dell T440 塔式服务器加装GPU

作者WellLee

【背景】

【知识框体】

【对判别法的一些补充】

1、一元函数极值判别法

①第一判别法f′(x0)=0

②第二判别法

2、多元函数极值判别法（针对条件极值）

①拉格朗日乘数法求极值

②定积分法求极值

【总结】

【参考文献】

作者 WellLee

相关文章

发表回复 取消回复

You missed

①第一判别法 $f^{'} (x_{0}) = 0$

发表回复取消回复