【CapsNet】Stacked Capsule Autoencoders

【0 Backgroud】

    在文章中我们介绍了Capsule的基本概念以及训练Capsules的动态路由算法。而20年初Hinton老爷子再一次将Capsule工作推进了一个档次。论文《Stacked Capsule Autoencoders》将Capsule应用于无监督网络，在MNIST上取得了最为先进的效果。

【1 开篇简介】

    相对于传统的不具备权值共享的神经网络，卷积神经网络在最近的AI领域中具有更好的效果。而神经网络归功于它能归纳偏差（inductive bias）：如果某一局部特征在图像的某个位置被检测到，那么在其他位置也肯能会被检测到。（如，在检测一副人脸图像时，我们在A图中检测到人的嘴巴特征， 那么我在B图中也有可能检测到同样的嘴巴特征，见下图）

    但也因为CNN具有这样的性质，因为CNN只负责检测物体的存在性，很少考虑其位置的合理性，这直接导致了传统的CNN鲁棒性不强。诚然，也有一些研究者尝试通过放缩、平移、旋转等一系列的方法来增强CNN模型的鲁棒性，但这也直接导致了高维特征图显得十分的臃肿。

    跨非平移自由度复制特征(replicating features across the non-translational degrees of freedom)的一种替代方法是显式学习整个对象的自然坐标框架与其每个部分的自然坐标框架之间的转换。计算机图形学依靠这样的对象→零件坐标变换来以视点不变的方式表示对象的几何形状。而且，有充分的证据表明，与标准的CNN不同，人类的视觉还依赖于坐标系：在熟悉的物体上施加不熟悉的坐标系会给物体或物体的几何形状的识别带来挑战

    神经系统（人脑神经系统）可以学习推理物体，物体的零件和观察者之间的转换，但是每种转换都可能需要用不同的方式表示。对象关系（OP）是视点不变的，近似恒定的，可以通过学习的权重轻松地进行编码。对象（或部分）相对于观察者的相对坐标随视点（它们是视点等变的）而变化，并且可以通过神经激活轻松地进行编码。通过这种表示，单个对象的姿势由其与查看者的关系表示。因此，与在CNN中不同，表示单个对象并不需要跨空间复制神经激活。它仅并行处理两个（或多个）同一类型对象的不同实例，这需要模型参数和神经激活的空间复制。

    在本文中，我们提出了堆叠式胶囊自动编码器（SCAE），它具有两个阶段（见下图）。第一阶段，零件胶囊自动编码器（PCAE），将图像分割为组成部分，推断其姿势，并通过适当安排仿射变换的部分模板来重建图像。第二阶段，对象胶囊自动编码器（OCAE），尝试将发现的零件及其姿势组织成较小的一组对象。然后，这些对象尝试使用对每个零件的单独预测混合来重建零件姿态。每个对象囊通过将其姿势（对象-查看者关系（OV））乘以相关的对象-部分关系（OP），为每种混合物贡献成分。

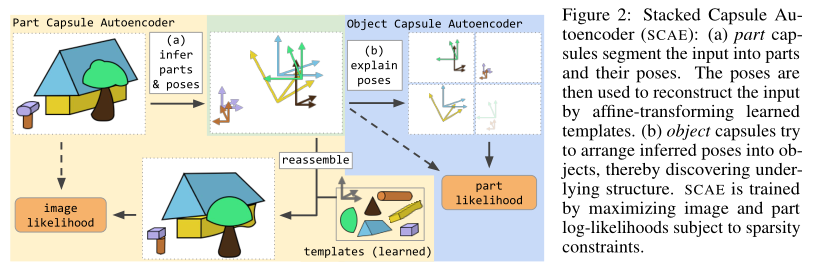
    堆叠式胶囊自动编码器在未经标记的数据上训练时，捕获了整个对象及其零件之间的空间关系。对象胶囊的存在概率向量趋向于形成紧密的簇（见下图），当我们为每个簇分配一个类时，对于SVHN的无监督分类（55％）和MNIST（98.7％），通过学习少于300个参数，可以分别进一步提高到67％和99％。有关代码，请访问：github传送门

【2 Stacked Capsule Autoencoders (SCAE)】

    将图像分割成多个部分并非易事，因此我们首先将像素和部分发现阶段抽象化，然后开发集群胶囊自动编码器（CCAE）。它使用二维点作为工具，并将其坐标作为系统的输入。
CCAE学习将点集建模为熟悉的集群排列，每个簇都通过独立的相似性变换进行了变换。
CCAE学会了将各个点分配给它们各自的簇，而无需事先知道簇的数量或形状。接下来我们开发了部件胶囊自动编码器（PCAE），该编码器学习从图像中推断零件及其姿势。最后，我们在PCAE上堆叠与CCAE非常相似的对象胶囊自动编码器（OCAE），以形成堆叠式胶囊自动编码器（SCAE）。

【2.1 Constellation Autoencoder (CCAE) – 群簇自编码器】

定义如下：

首先定义二维输入集合：$X_m|m=1,\dots ,M$，其中每个点属于下图中的每个簇，然后用Set Transformer 对所有的输入点进行编码，划分为$K$类目标胶囊（即将输入点编码成部分胶囊）。其中Set Transformer是一种注意力机制的排列不变编码器$h^{caps}$。

每个目标胶囊$k$由下面三部分

• 一个特征向量胶囊$c_k$

• 胶囊存在概率$a_k\in [0,1]$

• 一个$3\times 3$ 目标-观察者联系矩阵（Object-viewer-relationship matrix）：该矩阵表示目标（簇）和观察者之间的视觉仿射变换组成。

注意，每个对象胶囊每次仅代表一个对象。每个目标胶囊都使用独立的多层感知机（MLP）$h_k^{part}$从特征向量胶囊$c_k$去预测$N\le M$个候选部分。

而每个候选区域由三部分组成：

• 给定候选部分存在的条件概率$a_{k,n}\in [0,1]$

• 一个相关标量的标准偏差${\lambda }_k$

• 一个$3\times 3$ 目标-部分联系矩阵组成，该矩阵表示目标和候选部分之间的仿射变换。

候选区域的预测值${\mu }_{k,n}$由对象胶囊OV矩阵与对象OP矩阵的乘积给出。

我们将所有输入点建模为单个高斯混合模型，其中${\mu }_{k,n}$和${\lambda }_{k,n}$分别代表同性高斯分量(isotropic)的中心和标准差。而公式描述见下文：

$\begin{array}{rlr}O{V}_{1:K},c_{1:K},{\alpha }_{1:K}=h^{caps}(X_{1:M})& & \mathrm{预}\mathrm{测}\mathrm{目}\mathrm{标}\mathrm{胶}\mathrm{囊}\mathrm{的}\mathrm{参}\mathrm{数}(1)\\ O{P}_{k,1:N},{\alpha }_{k,1:N},{\lambda }_{k,1:N}=h_k^{part}(c_k)& & \mathrm{对}{c}_k\mathrm{产}\mathrm{生}\mathrm{的}\mathrm{候}\mathrm{选}\mathrm{参}\mathrm{数}\mathrm{进}\mathrm{行}\mathrm{解}\mathrm{码}(2)\\ V_{k,n}=O{V}_{k}O{P}_{k,n}& & \mathrm{对}\mathrm{部}\mathrm{件}\mathrm{姿}\mathrm{态}\mathrm{候}\mathrm{选}\mathrm{区}\mathrm{域}\mathrm{进}\mathrm{行}\mathrm{解}\mathrm{码}(3)\\ p(X_m|k,n)=\mathcal{N}(X_m|{\mu }_{k,n},{\lambda }_{k,n})& & \mathrm{将}\mathrm{候}\mathrm{选}\mathrm{区}\mathrm{域}\mathrm{分}\mathrm{类}\mathrm{至}\mathrm{混}\mathrm{合}\mathrm{部}\mathrm{件}\mathrm{中}(4)\end{array}$

    通过最大化方程（5）中的部件胶囊受稀疏性约束的影响，无需监督即可对模型进行训练，请参见。
2.4节和附录C。通过观察混合物成分公式:$k^{\ast }=\arg \underset{k}{max}{a}_k{a}_{k,n}p(X_m|k,n)$可以将部分胶囊$m$分配给目标胶囊$k^{\ast }$, 即使在难以为人类解释的数据中，它也能够对属于不同簇群的点执行无监督的实例级分割。有关示例，请参见图3，有关详细信息，请参见第3.1节。

$\begin{array}{r}p(X_{1:M})=\prod _{m=1}^M\sum _{K=1}^K\sum _{n=1}^N\frac{a_k{a}_{k,n}}{\sum _i{a}_i\sum _j{a}_{i,j}}p(X_m|k,n)(5)\end{array}$

【2.2 Part Capsule Autoencoder (PCAE)-部分胶囊自编码器】

    将图像解释为零件的几何排列需要1）发现图像中存在哪些零件，以及2）推断部件与观察者的关系（他们的姿势）。对于CCAE，零件只是2D点（即（x，y）坐标），但是对于PCAE，每个零件胶囊$m$具有六维姿态$X_m$（两次旋转，两次平移，缩放和剪切），存在变量$d_m\in [0,1]$和唯一身份。我们将部件发现问题归结为自动编码：编码器学会推断不同零件囊的姿势和存在，而解码器学习类似于Tieleman，2014的每个零件的图像模板$T_m$（图4） Eslami等人，2016。如果存在某个零件（根据其存在变量），则将相应的模板与推断的姿态给出${\hat{T}}_m$进行仿射变换。最后，将转换后的模板排列到图像中。PCAE之后是对象封装自动编码器（OCAE），该对象编码器非常类似于CCAE，在2.3节中进行了介绍。

定义如下：

    首先让: $y\in [0,1{]}^{h\times w\times c}$ 表示一副图像，我们将最大的部分胶囊数量限制为$\mathcal{M}$ 并用一个编码器去推理它们的姿态$X_m$、存在概率$d_m$和特征（ Special features ）$Z_x\in {\mathbb{R}}^{c_z}$,一个部分胶囊， 可以使用特殊特征（Special features ）以依赖于输入的方式更改模板（我们使用它们来预测颜色，但是可以进行更复杂的映射）。这些特殊特征（Special features ）还通知OCAE有关相应部分的独特方面（比如遮挡与其他部分的关系）。模板$T_m\in [0,1{]}^{h_t\times w_t\times (c+1)}$ 是小于图像$y$，但还有一个附加的Alpha通道，允许其他模板进行遮挡。我们使用$T_m^{\alpha }$指代alpha通道，使用$T_m^c$指代其颜色。

    我们允许每个零件囊仅使用一次来重建图像，这意味着相同类型的零件不会重复5。为了推断零件胶囊的参数，我们使用基于CNN的编码器，然后进行基于注意力的合并，这在附录E中有更详细的描述，其对模型性能的影响将在3.3节中进行分析。

    图像被建模为空间高斯混合模型类似于Greff等人2019年;Burgess等2019; Engelcke等人2019。我们的方法不同之处在于，我们使用变换后的模板的像素（而不是逐分量重构）作为各向同性高斯分量的中心，但是我们也使用恒定方差。不同成分的混合概率与部分胶囊的存在概率与每个模板的获悉alpha通道值的乘积成正比。公式如下：

    训练PCAE会得到对象部分的学习模板，在MNIST的情况下类似于笔画，请参见图4。通过最大化方程式（10的图像似然性来训练模型的这一阶段。

【2.3 Object Capsule Autoencoder(OCAE) 目标胶囊自编码器】

    在确定了某一目标的独立部分以及他们的参数（相对坐标）之后，我们就能根据这些参数以及各部件计算（推导）出它们。为此，我们使用级联姿势$X_m$、特殊特征$Z_m$和战平的模板$T_m$(传达部分胶囊的标识)作为OCAE的输入，与CCAE不同于以下方面：

1. 我们向OCAE编码器输入部分胶囊的存在概率$d_m$:用于偏置Set Transformer的注意力机制而不考虑缺失点。

2. $d_m$也用于衡量部件胶囊的对数似然。这样就不用考虑缺失点的对数似然，这是通过$m^{th}$的部件胶囊似然提高至$d_m，cf$来实现的。如式（5）

3. 值得一提的是，我们停止了所有OCAE输入的梯度，除了提高训练稳定性和避免潜在变量崩溃的特殊功能；参见e.g.，Rasmus等人，2015。最后，PCAE发现的零件具有独立的标识（模板和特殊特征，而不是二维点）。因此，每个部分姿势被解释为来自对象胶囊的预测的独立混合物，其中每个对象胶囊精确地生成M个候选预测$V_{k,1:M}$，或者每个部分精确地生成一个候选预测。因此，部分胶囊的可能性由式(11)给出：

$\begin{array}{r}p(X_{1:M},d_{1:M})=\prod _{m=1}^M[\sum _{k=1}^K\frac{a_k{a}_{k,m}}{\sum _i{a}_i\sum _j{a}_{i,j}}p(X_m|k,m){]}^{d_m}\end{array}(11)$

    OCAE通过最大化等式（11）的部分姿势可能性来训练，它学习在先前识别的部分中发现进一步的结构，从而学习稀疏激活的对象胶囊，见图5。然而，实现这种稀疏性需要进一步的正则化。

【2.4 Achieving Sparse and Diverse Capsule Presences】

    堆叠的胶囊自动编码器被训练成最大化像素和部分对数（${\mathcal{L}}_{11}=\log p(y)+\log p(X_{1:M})$）,但是，如果不受约束，他们倾向于使用所有部分和对象胶囊来解释每个数据示例，或者不管输入是什么，总是使用相同的胶囊子集。我们希望模型为不同的输入示例使用不同的零件胶囊集，并将对象胶囊专门化为零件的特定排列。为了鼓励这一点，我们施加了稀疏性和熵约束。我们在第3.3节中评估了它们的重要性。我们首先定义了先前和之后的物体胶囊存在如下。对于一小批大小为$B$的$K$个对象胶囊和$M$个部分胶囊，我们定义了一小批使用稀疏性和熵约束前的胶囊存在概率$a_{1:K}^{\mathrm{prior}}$(shape 为$[B,K]$)和使用后的胶囊存在概率为$a_{1:K,1:M}^{\mathrm{posterior}}$（shape为$[B,K,M]$）具体定义如下：

$\begin{array}{rlr}{a}_k^{\mathrm{prior}}=a_k\underset{m}{max}{a}_{m,k},& & a_{k,m}^{\mathrm{posterior}}=a_k{a}_{k,m}\mathcal{N}(X_m|m,k)\end{array}(12)$

    前者是目标胶囊$k$预测的最大存在概率，后者是用于解释部分胶囊$m$的非标准化混合比例

Prior sparsity

    我们让$\begin{array}{r}{\overline{u}}_k=\sum _{b=1}^B{a}_{b,k}^{\mathrm{prior}}\end{array}$表示不同训练实例中目标胶囊k存在概率之和，$\begin{array}{r}{\hat{u}}_b=\sum _{k=1}^K{a}_{b,k}^{prior}\end{array}$表示一个给定例子的目标胶囊存在概率之和，如果我们假设训练示例中包含来自不同类的对象，并且我们希望为每个类分配相同数量的对象胶囊，那么每个类将获得k/C胶囊。此外，如果我们假设每个图像中只存在一个对象，那么对于每个输入示例，应该存在k/C对象胶囊，这将导致每个对象胶囊存在b/C的概率之和。为此，我们尽量按照下式最小化损失。

$\begin{array}{r}{\mathcal{L}}_{\mathrm{prior}}=\frac{1}{B}\sum _{b=1}^B({\hat{u}}_b–K/C{)}^2+\frac{1}{K}\sum _{k=1}^K({\overline{u}}_k–B/C{)}^2\end{array}(13)$

Posterior Sparsity

    类似地，我们试验了最小化胶囊后位存在$\mathcal{H}({\overline{v}}_k)$的实例内熵和最大化其实例间熵$\mathcal{H}({\hat{v}}_b)$，其中$\mathcal{H}$是熵，其中${\overline{v}}_k\mathrm{和}{\hat{v}}_b$分别是$\begin{array}{r}\sum _{k,m}{a}_{b,k,m}^{\mathrm{posterior}}\end{array}$和$\begin{array}{r}\sum _{b,m}{a}_{b,k,m}^{\mathrm{posterior}}\end{array}$的标准化版本。最后的损失是:

$\begin{array}{r}{\mathcal{L}}_{\mathrm{posterior}}=\frac{1}{K}\sum _{k=1}^K\mathcal{H}({\overline{v}}_k)–\frac{1}{B}\sum _{b=1}^B\mathcal{H}({\hat{v}}_b)\end{array}(14)$

    然而，我们的消融研究表明，在没有这些后稀疏约束的情况下，该模型的表现同样良好，参见第3.3节。

    图6为SCAE的结构示意图。我们对图像的加权和、部分概率和辅助损失进行了优化。减重的选择过程以及实验所用的数值详见附录A。

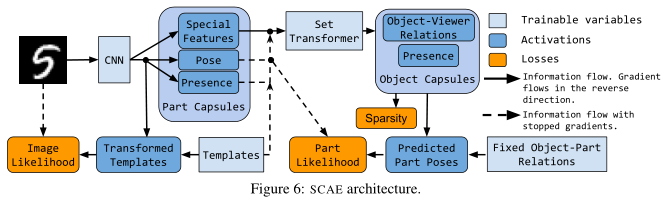
【实验评估（略）】

【总结】

    我们的工作的主要贡献是一种新的表示学习方法，其中使用高度结构化的解码器网络来训练一个编码器网络，它可以将图像分割成部分和它们的姿态，另一个编码器网络可以将部分组成连贯的整体。尽管我们的训练目标与分类或聚类无关，但SCAE是在无监督对象分类中不依赖互信息(MI)而获得竞争结果的唯一方法。这一点很重要，因为与我们的方法不同，基于mi的方法需要复杂的数据扩充。利用基于mi的损失训练SCAE可能会进一步改善结果，其中胶囊概率向量可以在IIC中扮演离散概率向量的角色(Ji et al.2018)。SCAE在CIFAR10上表现不佳，这可能是因为使用了固定模板，而固定模板的表达能力不足以对实际数据建模。这可以通过构建更深层的胶囊自动编码器来解决。在计算机图形学中，复杂的场景被建模为仿射变换的几何原语的深树)，以及使用依赖输入的形状函数而不是固定模板——这两者都是未来工作的有希望的方向。也可以通过在生成模型中使用可微分的呈现器(从原始胶囊中重建像素)来制作更好的PCAE来学习原始胶囊。最后，SCAE可以是混合模型的“图形”组件，它还包括一个通用的“地面”组件，可以用来解释除图形之外的所有东西。一个复杂的图像，然后可以分析使用顺序注意，以感知一个数字在一个时间。

【参考文献】

• Adam R. Kosiorek,Sara Sabour,Y ee Whye Teh, Geoffrey E. Hinton. Stacked Capsule Autoencoders. NIPS-2019