基本形式:
对于任何实数 \(a,b\) 的所谓的著名三角不等式:
\( \left|a\right| + \left|b\right| \leq \left| a + b \right|\)
其等价形式为:
\( |\alpha-\beta|\leq |\alpha-\gamma|+|\gamma-\beta| \)
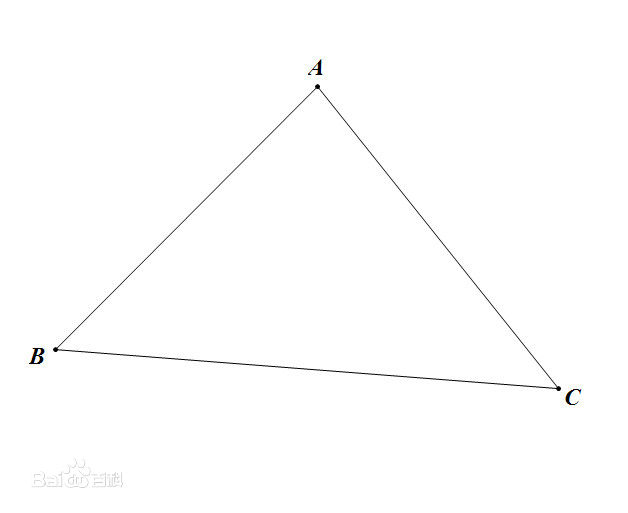
简单证明,令\( a=\alpha-\gamma, b=\gamma-\beta\),得证。等价形式对应的实际几何意义在于,从\(\alpha\)到 \(\gamma\)的直达距离,小于或等于经过第三点(转折)的两短距离之和。当然,这一不等式还可对应于这样的基本事实,在任何三角形,两边之和大于第三边
。
扩展:
两数之间的关系,自然可以推广到三个数,乃至无线多个数之间的关系。
\(|a_1+a_2+\cdots+a_n|\leq |a_1|+|a_2|+\cdots+|a_n|\)
可通过数学归纳法进行证明:
\(|a_1+a_2+\cdots+a_{n-1}| \leq |a_1|+\cdots+|a_{n-1}|\)
因此:
\(|a_s+a_n|\leq |a_s|+|a_n|\)(令\(a_s=a_1+\cdots+a_{n-1}\))
\(|a|=|(a+b)-b|\leq |a+b|+|-b|=|a+b|-|b|\)
因此:
\(|a|-|b|\leq |a+b|\leq |a|+|b|\)
根据对称性,显然:\(a\Leftrightarrow b\)得:
\(|b|-|a|\leq |a+b|\leq |a|+|b|\)