极限:
“极限”是数学中的分支——微积分的基础概念,广义的“极限”是指“无限靠近而永远不能到达”的意思。数学中的“极限”指:某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”(“永远不能够等于A,但是取等于A‘已经足够取得高精度计算结果)的过程中,此变量的变化,被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”(当然也可以用其他符号表示)。
思维导图:
一、数列极限:
定义:
引论:
性质:
唯一性:
利用反证法证明:
保号性:
证明:
有界性:
二、函数极限
1.自变量趋于有限值
Notes:
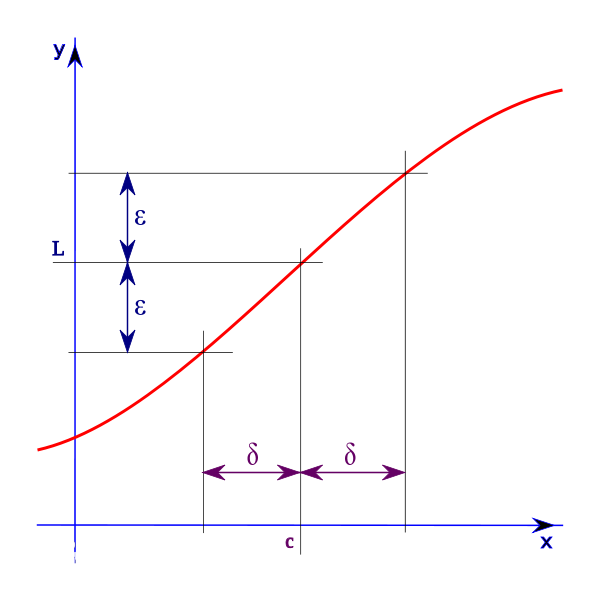
定义:
Notes:
2.自变量趋于无穷大
Notes:
性质:(两种情况都成立,无论是自变量趋于有限值还是无穷大)
唯一性:
保号性:
证明:
三、无穷小与无穷大
1、无穷小
定义
简单来说,以零为界限就称为无穷小。
Notes
零是无穷小,但无穷小不一定是零
非零函数是否无穷小与它的自变量趋势有关
例如:
性质
①
证明:
②
证明:
③
证明:
④
证明:
2、无穷大
关于无穷大的定义与性质可以用一句话概括:无穷大即无穷小的倒数,欲证明其定义与性质只需证明无穷小的倒数即可
四、参考文献
-
《高等数学》第七版-上册 同济大学数学系 编
屌爆了,差点没发现是个人网站