【背景】
随机变量(random variable)表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表达。
随机事件数量化的好处是可以用数学分析的方法来研究随机现象。
【基础定义】
1、随机变量:
2、分布函数:
2.1)性质(充要条件):
2.2) 注解:
3. 离散型随机变量
分布律:
| x | |
| p |
4. 连续型随机变量
4.1) 定义
【常见的随机变量】
记录实验过程
【背景】
随机变量(random variable)表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表达。
随机事件数量化的好处是可以用数学分析的方法来研究随机现象。
【基础定义】
在 样 本 空 间 中 , 唯 一 的 与 对 应 , 则 称 为 随 机 变 量
为 随 机 变 量 , 称 为 的 分 布 函 数
2.1)性质(充要条件):
① ② 不 减 ③ 右 连 续 ; ④
2.2) 注解:
设 为 分 布 函 数 ① ② ③ ④
分布律:
| x | |
| p |
4.1) 定义
随 机 变 量 , 使 得 称 为 连 续 性 随 机 变 量 其 中 为 密 度 函 数 , 连 续 , 但 不 一 定 可 导
【常见的随机变量】
若 随 机 变 量 的 分 布 律 为 : 则 称 服 从
若 随 机 变 量 的 分 布 律 为 : 则 称 服 从
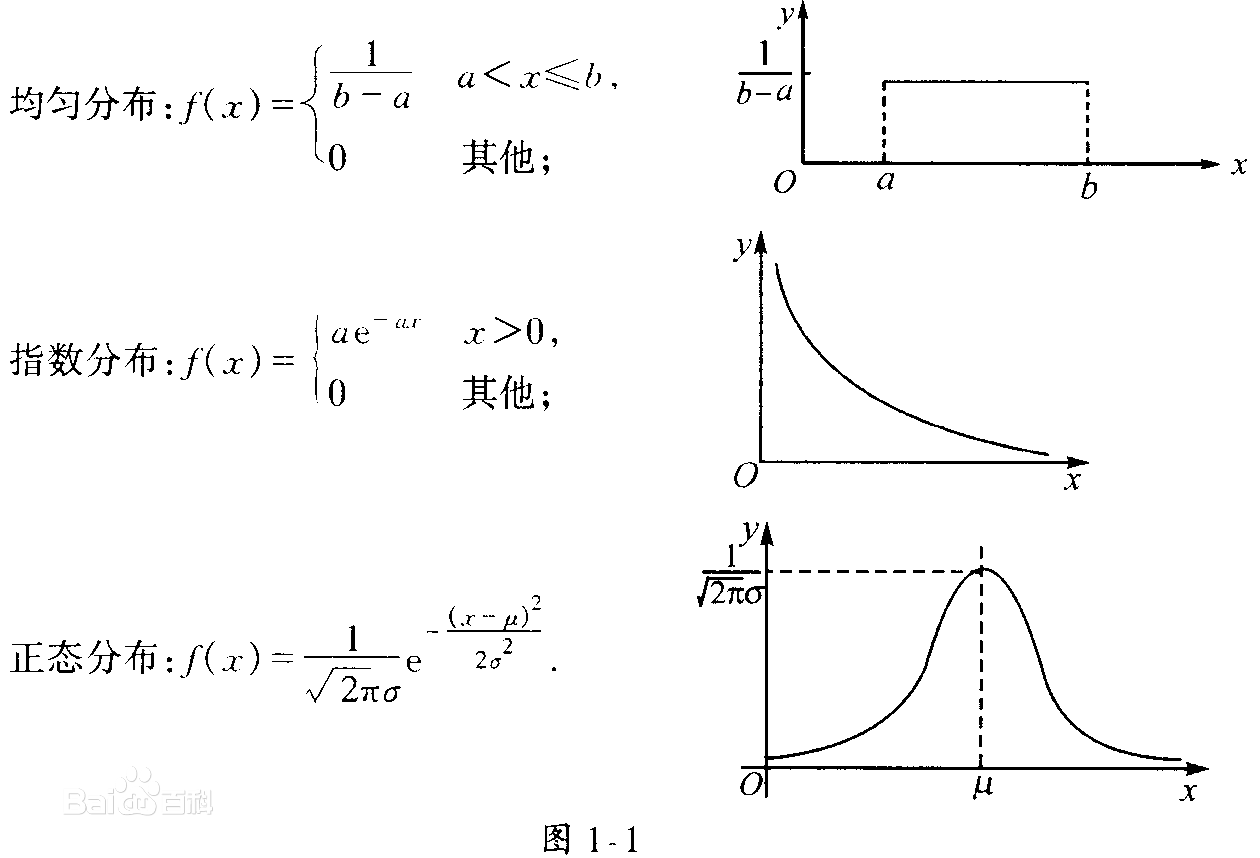
若 随 机 变 量 的 密 度 函 数 为 : 其 他 则 称 服 从 于 其 分 布 函 数 如 下 :
若 随 机 变 量 的 密 度 函 数 为 : 则 称 服 从 于 其 分 布 函 数 如 下 注 解 : 服 从 于 则
若 随 机 变 量 的 密 度 函 数 为 : 则 称 服 从 于 特 别 地 , 如 果 即 称 服 从 标 准 正 态 分 布 若 服 从 于 标 准 正 态 分 布 , 则 注 解 ① 服 从 正 态 分 布 , 则 ② ③ 服 从 正 态 分 布