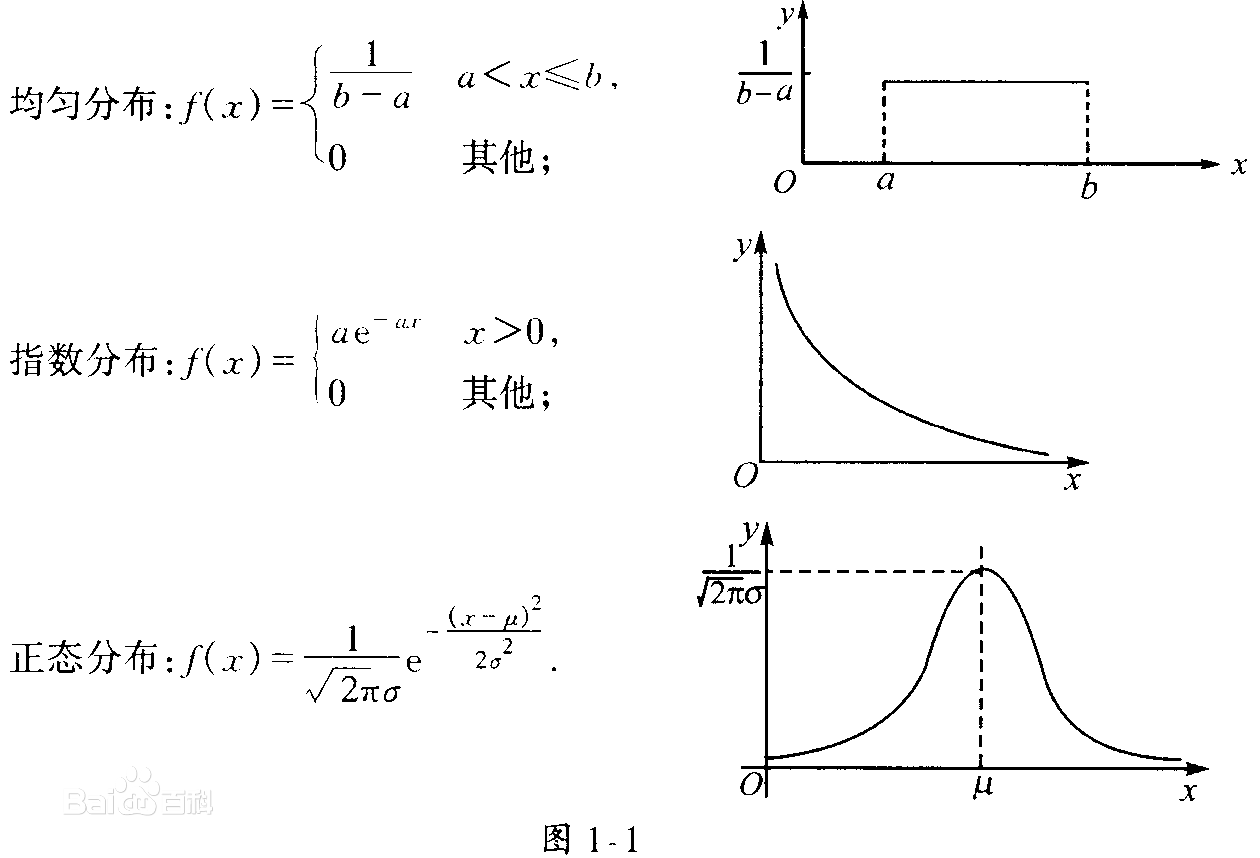
【背景】
特征是一个客体或一组客体特性的抽象结果。特征是用来描述概念的。任一客体或一组客体都具有众多特性，人们根据客体所共有的特性抽象出某一概念，该概念便成为了特征。而数字特征是对于数字的一种抽象方式，不同的抽象方式表现数字不同方面的数字特征（如，均值表现平均水平，方差表示离散程度）。从信息的角度来说，特征化（抽象）是压缩信息的一种方式。
为何会有数字特征？特征化是人们压缩数据的一种方式，它能够反映一些群体的某方面的特点。举个简单的例子，校长去某个班调查学生的学习水平，他不太可能去查看询问每个人的成绩（那样子是十分耗时的一件事情）。所以我们将班级的成绩信息进行压缩，压缩成均值，众数，标准差等，以此来为校长提供其所关心的平均水平，成绩差异程度等。
【数学期望（均值）】
<1>定义：
1、对于一元离散型随机变量：
已知分布律：
X
\(x_1,x_2, \cdots , x_n\)
P
\(p_1,p_2,\cdots, p_n\)
\(\begin{align} &则有数学期望：E(X)=x_1p_1 + x_2p_2 + \cdots + x_n p_n \\& 若Y=\varphi(x) 则\\& E(Y)= \sum_{i=1}^{n} \varphi(x_i) p_i\end{align}\)
2、对于一元连续性随机变量：
\(\begin{align}& 已知X服从于f(x) \\&E(X)=\int_{-\infty}^{+\infty} x f(x) dx \\&若Y=\varphi(x) 则\\& E(Y) = \int_{-\infty}^{+\infty} \varphi(x) f(x) dx\end{align}\)
3、对于二元离散型随机变量：
\(\begin{align}&P\{X = x_i,Y=y_j\} = p_{ij}(i = 1,2,\cdots,m)(j = 1,2,\cdots,n) \\& Z = \varphi(X,Y) 则\\&E(Z)=\sum_{i=1}^{m} \sum_{j=1}^{n} \varphi(x_i,y_i) p_{ij}\end{align}\)
4、对于二元连续性随机变量：
<1>定义
\(\begin{align}&已知(X,Y)服从于f(x,y) \\&Z = \varphi(X,Y) \\&E(Z)=\int_{-\infty}^{+\infty}dx \int_{-\infty}^{+\infty} \varphi(x,y)f(x,y)dy \end{align}\)
<2>性质：
\(\begin{align}&1.E(c) = c \\&2.E(kX) = kE(X) \\&3.E(X+Y) = E(X)+E(Y)\\&4.若X,Y独立\rightarrow 则E(XY) = E(X) \cdot E(Y) \end{align}\)
【方差】
<1>定义：
\(\begin{align}&D(X)=E(X-EX)^2\end{align}\)
<2>计算公式：
\(\begin{align}&D(X)=E(X^2) – (EX)^2\end{align}\)
<3>性质：
\(\begin{align}&1.D(C) = 0 \\&2.D(kX) = k^2DX \\&若X,Y独立\rightarrow D(aX+bY) = a^2D(X) + b^2D(Y) \end{align}\)
<4>常见随机变量的数学期望与方差:
\(\begin{align}&1、X服从于B(n,p): \\& P\{X=k\} = C_n^kP^k(1-p)^{n-k}(k=0,1,2, \cdots,n ) \\&E(X) = np, D(X)=np(1-p)\\ \\&2.X服从于\pi(\lambda)(\lambda > 0)\\&P\{X=k\} = \frac{\lambda^k}{k!} e^{-\lambda} (k=0,1,2,\cdots) \\&E(X) = \lambda, D(X)=\lambda \\ \\&3.X服从于G(p) (0<p<1) (几何分布) \\& P\{X=k\} = p(1-p)^{k-1} (k=1,2,\cdots) \\& E(X)= \frac{1}{p},D(X)=\frac{1-p}{p^{2}} \\ \\&4.X服从于U(A,B) \\&f(x) = \begin{cases}\frac{1}{b-a} &a<x<b \\ 0&其他\end{cases}\\&E(X) = \frac{a+b}{2}.D(X)=\frac{(b-a)^2}{12} \\ \\&5.X服从于E(\lambda) (\lambda >0) \\& f(x) = \begin{cases} \lambda e^{-\lambda x} & x >0 \\ 0 & x \leq 0 \end{cases} \\&F(x) = \begin{cases} 1 – e^{-\lambda x} &x \geq 0 \\ 0 & x < 0\end{cases} \\& E(X) = \frac{1}{\lambda}, D(X) = \frac{1}{\lambda^2} \\ \\&6.X服从于N(0,1) \\&f(x) = \frac{1}{\sqrt{2\pi}}e ^{-\frac{x^2}{2}} \\&E(X)=0,D(X)=1\\&X服从于N(\mu,\sigma) \\&f(x) = \frac{1}{\sqrt{2\pi} \sigma}e^{-\frac{(x – \mu)^2}{2\sigma}} \\&E(X)=\mu,D(X)=\sigma ^2\end{align}\)
【协方差与相关系数】
<1>协方差
\(\begin{align}&1.定义:\\&D(X)=E(X-EX)^2 = E(X-EX)(Y-EY) \\ \\&2.计算公式: \\&Cov(X,Y) =E(XY) – E(X)\cdot E(Y) \\ \\&3.性质:\\&①Cov(X,X) = D(X) \\ \\&②Cov(X,Y) =Cov(Y,X) \\ \\&③Cov(aX,bY) = abCov(X,Y) \\ \\&④Cov(X,k_1Y_1+\cdots+k_n Y_n) = k1Cov(X_1,Y_1) + \cdots + k_nCov(X,Y_n) \\ \\&⑤D(aX+bY) = Cov(aX+BY,aX+bY) \\ & =a^2Cov(X,X) + 2abCov(X,Y) + b^2Cov(Y,Y) \\&=a^2D(X)+2abCov(X,Y)+ b^2D(Y)\end{align}\)
<2>相关系数
\(\begin{align}&1.定义\\&\rho_{XY} = \frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}} \\ \\&2.性质\\&① |\rho_{XY}| \leq 1 \\ \\&②如果:\rho_{xy} = -1\rightarrow 称X,Y负相关 \\& \rho_{XY} = -1 \Leftrightarrow P\{Y=ax+b\} = 1 (a < 0)\\ \\&③如果：\rho_{XY} = 1 \rightarrow 称X，Y正相关 \\& \rho_{XY} = 1 \Leftrightarrow P\{Y=ax+b\} = 1(a>0) \\ \\&④如果：\rho_{XY} = 0 \rightarrow 称X,Y不相关\\& \rho_{XY}=0 \Leftrightarrow Cov(X,Y) = 0 \Leftrightarrow E(XY) = E(X)\cdot E(Y) \\ \\&⑤X,Y独立 \Rightarrow E(X) \cdot E(Y) = E(XY) \Rightarrow \rho_{XY} =0 \\&即X,Y独立 \Rightarrow X，Y不相关 \\ \\&⑥(X,Y) 服从于N(\mu _1,\mu _2,\sigma _1^2,\sigma _1^2 ,\rho)则\\&X,Y独立\Leftrightarrow X,Y不相关 \Leftrightarrow \rho_{XY} = 0 \end{align}\)
【参考文献】
文章导航
