【背景】
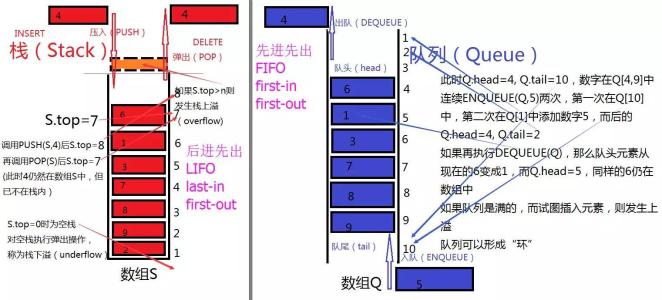
栈（stack）又名堆栈，它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。
【源码运行环境】
操作系统：MAC OS X 10.13.4
编译环境：CLion (C++ 14) cmake
【源码实现】
S_Q.h源码部分：
//
// Created by WellLee on 2018/10/29.
//
#ifndef STACK_Queue_S_Q_H
#define STACK_Queue_S_Q_H
#include "stdio.h"
#include "stdlib.h"
#include "memory.h"
/*
* 说明：define 定义一些常用的符号特性
* 作用：增加代码可读性
* Author: WellLee
* Last Modified: 2018年10月31日23:16:07
*/
#define TRUE 1
#define FALSE 0
#define OVERFLOW -1
#define MAXSIZE 20
typedef int Status;
typedef int Elem;
/*
* 结构：顺序栈
* 作用：定义了顺序栈的一些结构特性，封装了常用的线性表操作
* Author: WellLee
* Last modified: 2018年10月31日23:17:31
*/
typedef struct Stack{
Elem data[MAXSIZE];
int top;
}Stack;
Status InitStack(Stack *S);
Status pop(Stack *S, Elem *e);
Status push(Stack *S, Elem e);
Status EmptyStack(Stack S);
Status ClearStack(Stack *S);
Status StackLength(Stack *S, int *length);
Status DestroyStack(Stack *S);
void showStackElements(Stack S);
/*
* 结构：链栈
* 作用：定义了链栈的一些结构特性，封装了常用的线性表操作
* Author: WellLee
* Last modified: 2018年10月31日23:17:31
*/
typedef struct Stacknode{
Elem elem;
struct Stacknode *next;
}stacknode,*StackNode;
typedef struct LinkStack{
StackNode top;
int length;
}*LStack;
Status InitLinkStack(LStack *LS);
Status LS_push(LStack *LS, Elem e);
Status LS_pop(LStack *LS, Elem *e);
Status LS_Clear(LStack *LS);
Status LS_Destroy(LStack *LS);
Status LS_Empty(LStack LS);
void LS_show(LStack LS);
/*
* 结构：顺序队列
* 作用：定义了顺序队列的一些结构特性，封装了常用的线性表操作
* Author: WellLee
* Last modified: 2018年10月31日23:17:31
*/
typedef struct SequenceQueue{
Elem data[MAXSIZE];
int front;
int rear;
}SqQueue;
Status InitSqQueue(SqQueue *Q);
Status EnSqQueue(SqQueue *Q, Elem e);
Status DeSqQueue(SqQueue *Q, Elem *e);
Status ClearSqQueue(SqQueue *Q);
Status DestroySqQueue(SqQueue *Q);
Status QueueLength(SqQueue Q, int *length);
void showQueueElements(SqQueue Q);
/*
* 结构：链队列
* 作用：定义了链队列的一些结构特性，封装了常用的线性表操作
* Author: WellLee
* Last modified: 2018年10月31日23:17:31
*/
typedef struct QueueNode{
Elem data;
struct QueueNode *next;
}QNode,*QNodeptr;
typedef struct LinkQueue{
QNodeptr rear;
QNodeptr front;
}LinkQueue;
Status InitLkQueue(LinkQueue *Q);
Status EnLkQueue(LinkQueue *Q, Elem e);
Status DeLkQueue(LinkQueue *Q, Elem *e);
Status ClearLkQueue(LinkQueue *Q);
Status DestroyLkQueue(LinkQueue *Q);
Status LkQueueLength(LinkQueue Q, int *length);
void showLkQueue(LinkQueue Q);
#endif //STACK_Queue_S_Q_H
Stack.c源码部分：
//
// Created by WellLee on 2018/10/29.
//
#include "S_Q.h"
#include "time.h"
/*
* 方法名：InitStack
* 作用：初始化顺序栈
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status InitStack(Stack *S)
{
S->top = -1;
int StackLength = 0;
Elem elem;
srand(time(0));
printf("请输入栈的元素个数");
scanf("%d", &StackLength);
for (int i = 0; i < StackLength; i++) {
elem = rand() % 100 - 1;
push(&*S, elem);
}
return TRUE;
}
/*
* 方法名：push
* 作用：顺序栈压栈操作
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status push(Stack *S, Elem e)
{
if(S->top >= MAXSIZE)
{
printf("栈满\n");
return OVERFLOW;
}
S->data[++S->top] = e;
return TRUE;
}
/*
* 方法名：StackEmpty
* 作用：判断顺序栈是否为空
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status StackEmpty(Stack S)
{
if(S.top == -1)
{
return TRUE;
}
return FALSE;
}
/*
* 方法名：pop
* 作用：顺序栈出栈操作
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status pop(Stack *S, Elem *e)
{
if(StackEmpty(*S))
{
printf("栈空\n");
return FALSE;
}
int top = S->top;
*e = S->data[S->top--];
S->data[top] = 0;
return TRUE;
}
/*
* 方法名：showStackElements
* 作用：显示顺序栈元素
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
void showStackElements(Stack S)
{
if(StackEmpty(S))
{
printf("栈空\n");
return;
}
printf("栈元素如下:");
printf("栈顶指向 -> %d \n",S.top);
for(int i = 0; i <= S.top; i++){
printf("%d ",S.data[i]);
}
printf("\n");
}
/*
* 方法名：DestroyStack
* 作用：销毁顺序栈
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status DestroyStack(Stack *S)
{
free(S);
return TRUE;
}
/*
* 方法名：ClearStack
* 作用：清空顺序栈
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status ClearStack(Stack *S)
{
memset(S->data,0, sizeof(S->data));
S->top = -1;
return TRUE;
}
/*
* 方法名：StackLength
* 作用：获取顺序栈长度
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status StackLength(Stack *S, int *length)
{
*length = S->top + 1;
return TRUE;
}
/*
* 方法名：InitLinkStack
* 作用：初始化链栈
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status InitLinkStack(LStack *LS)
{
srand(time(0));
StackNode head = (StackNode)malloc(sizeof(stacknode));
if(!head)
{
printf("内存不足\n");
return OVERFLOW;
}
head->next = NULL;
*LS = (LStack)malloc(sizeof(LStack));
if(!*LS)
{
printf("内存不足\n");
return OVERFLOW;
}
LStack ls = *LS;
ls->top= head;
ls->length = 0;
printf("请输入栈的元素个数:");
int length;
scanf("%d", &length);
for(int i = 0; i < length; i++)
{
Elem e = rand()%100 -1;
LS_push(&ls, e);
}
printf("初始化成功\n");
return TRUE;
}
/*
* 方法名：LS_push
* 作用：链栈压栈操作
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status LS_push(LStack *LS, Elem e)
{
LStack ls = *LS;
if(!ls)
{
printf("线性表参数有误\n");
return OVERFLOW;
}
StackNode head = ls->top;
StackNode elem = (StackNode)malloc(sizeof(stacknode));
if(!elem)
{
printf("内存不足\n");
return OVERFLOW;
}
elem->elem = e;
elem->next = ls->top->next;
head->next = elem;
ls->length++;
printf("%d 入栈\n", e);
return TRUE;
}
/*
* 方法名：LS_pop
* 作用：链栈出栈操作
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status LS_pop(LStack *LS, Elem *e)
{
if(LS_Empty(*LS))
{
printf("空栈,无元素出栈\n");
return OVERFLOW;
}
LStack ls = *LS;
StackNode node = ls->top;
StackNode freenode = node->next;
*e = freenode->elem;
node->next = freenode->next;
free(freenode);
ls->length--;
printf("%d 出栈\n", *e);
return TRUE;
}
/*
* 方法名：LS_Clear
* 作用：清空链栈
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status LS_Clear(LStack *LS)
{
LStack ls = *LS;
if(!ls){
printf("栈参数有误\n");
return FALSE;
}
while(ls->length != 0)
{
Elem temp;
LS_pop(&ls, &temp);
}
printf("栈已清空\n");
return TRUE;
}
/*
* 方法名：LS_Destroy
* 作用：销毁链栈
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status LS_Destroy(LStack *LS)
{
free(*LS);
printf("栈已销毁\n");
return TRUE;
}
/*
* 方法名：LS_Empty
* 作用：判断链栈是否为空
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
Status LS_Empty(LStack LS)
{
if(LS->length == 0)
{
return TRUE;
}
return FALSE;
}
/*
* 方法名：LS_show
* 作用：显示链栈元素
* Author: WellLee
* Last Modified:2018年10月31日23:21:09
*/
void LS_show(LStack LS)
{
if(LS_Empty(LS))
{
printf("空栈\n");
return;
}
StackNode head = LS->top->next;
printf("当前栈有%d个元素，如下所示:\n",LS->length);
while(head!=NULL)
{
printf("%d ",head->elem);
head = head->next;
}
printf("\n");
}
Queue.c 源码如下
//
// Created by WellLee on 2018/10/31.
//
#include "S_Q.h"
/*
* 方法名：InitSqQueue
* 作用：初始化顺序队列
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status InitSqQueue(SqQueue *Q)
{
Q->front = 0;
Q->rear = 0;
return TRUE;
}
/*
* 方法名：EnSqQueue
* 作用：顺序队列入队操作
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status EnSqQueue(SqQueue *Q, Elem e)
{
if((Q->rear + 1) % MAXSIZE == Q->front)
{
printf("队列满\n");
return OVERFLOW;
}
Q->data[Q->rear] = e;
Q->rear = (Q->rear+1) % MAXSIZE;
return TRUE;
}
/*
* 方法名：DeSqQueue
* 作用：顺序队列出队操作
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status DeSqQueue(SqQueue *Q, Elem *e)
{
if(Q->rear == Q->front)
{
printf("队空\n");
return FALSE;
}
*e = Q->data[Q->front];
Q->front = (Q->front + 1) % MAXSIZE;
}
/*
* 方法名：ClearSqQueue
* 作用：清空顺序队列
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status ClearSqQueue(SqQueue *Q)
{
memset(Q->data,0, sizeof(Q->data));
InitSqQueue(Q);
return TRUE;
}
/*
* 方法名：DestroySqQueue
* 作用：销毁顺序队列
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status DestroySqQueue(SqQueue *Q)
{
ClearSqQueue(Q);
printf("队列已经销毁\n");
return TRUE;
}
/*
* 方法名：QueueLength
* 作用：获取顺序队列长度
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status QueueLength(SqQueue Q, int *length)
{
*length = (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
return TRUE;
}
/*
* 方法名：showQueueElements
* 作用：输出顺序队列中的元素
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
void showQueueElements(SqQueue Q)
{
int length = 0;
QueueLength(Q, &length);
if(length == 0)
{
printf("队空\n");
return;
}
printf("当前队列元素如下\n");
for(int i = 0; i < length; i++)
{
printf("%d ", Q.data[Q.front + i]);
}
printf("\n");
}
/*
* 方法名：InitLkQueue
* 作用：初始化链队
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status InitLkQueue(LinkQueue *Q)
{
QNodeptr head = (QNodeptr )malloc(sizeof(QNode));
if(!head)
{
printf("内存不足\n");
return OVERFLOW;
}
head->next = NULL;
Q->front = head;
Q->rear = head;
return TRUE;
}
/*
* 方法名：EnLkQueue
* 作用：链队压栈操作
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status EnLkQueue(LinkQueue *Q, Elem e)
{
QNodeptr node = (QNodeptr )malloc(sizeof(QNode));
if(!node)
{
printf("内存不足\n");
return OVERFLOW;
}
node->data = e;
node->next = NULL;
Q->rear->next = node;
Q->rear = node;
return TRUE;
}
/*
* 方法名：DeLkQueue
* 作用：链队出栈操作
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status DeLkQueue(LinkQueue *Q, Elem *e)
{
if(Q->rear == Q->front)
{
printf("队空\n");
return FALSE;
}
QNodeptr temp = Q->front->next;
Q->front->next = temp->next;
*e = temp->data;
if(Q->front->next == NULL)
{
Q->rear = Q->front;
}
free(temp);
return TRUE;
}
/*
* 方法名：ClearLkQueue
* 作用：清除链队所有数据
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status ClearLkQueue(LinkQueue *Q)
{
while(Q->front != Q->rear)
{
Elem temp;
DeLkQueue(Q, &temp);
}
return TRUE;
}
/*
* 方法名：DestroyLkQueue
* 作用：销毁链队
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status DestroyLkQueue(LinkQueue *Q)
{
free(Q->front);
return TRUE;
}
/*
* 方法名：LkQueueLength
* 作用：获取链队元素长度
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
Status LkQueueLength(LinkQueue Q, int *length)
{
QNodeptr temp = Q.front->next;
int i = 0;
while(temp != NULL)
{
i++;
temp = temp->next;
}
*length = i;
}
/*
* 方法名：showLkQueue
* 作用：显示链队所有元素
* Author: WellLee
* Last Modified:2018年10月31日23:42:16
*/
void showLkQueue(LinkQueue Q)
{
QNodeptr temp = Q.front;
temp = temp->next;
if(temp == NULL)
{
printf("队空\n");
return;
}
printf("队列元素如下\n");
while(temp != NULL)
{
printf("%d ",temp->data);
temp = temp->next;
}
}
【分析】
-
栈和队列都是特殊的线性表，只不过是对插入和删除做了限制。
-
栈（Stack）是限定仅在表尾进行插入和删除操作的线性表。根据这样的特性又可以称它为：后进先出表（LIFO）。
-
队列（Queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。根据这样的特性又可以称它为：先进先出表（FIFO）。
-
它们均可以用线性表顺序存储结构来实现，但都存在顺序存储的一些弊端，因此它们各自有各自的技巧来解决这个问题。
-
对于栈来说，如果是两个相同数据类型的栈，可以用数组的两端作为栈底的方法来让两个栈共享数据，这就可以最大化利用数组的空间。
-
对于队列来说，为了避免数组插入和删除时需要移动数据，于是引进了循环队列，使得队头和队尾可以在数组中循环变化。解决了移动数据的时间损耗，使得原来的删除和插入式O(n)的时间复杂度编程了O(1)。
-
它们也都可以用链式存储来实现，实现原则上与线性表基本相同。
【总结】
本文通过学习栈和队列两种数据结构的定义，性质和实现方式，给出了栈/队列的C语言程序实现。加深了对栈/队列的认识，也接触了一些栈在计算机中的应用（递归，中缀->后缀表达式等）。也在从线性表表示栈/队列过程中学习到了一些前人解决问题的思想（共享栈、循环队列的引入）。而这两种数据结构的引入简化了程序设计的问题，划分了不同关注层次，使得思考范围缩小，更更加聚焦于我们要解决问题的核心。
【参考文献】
《大话数据结构》.程杰.清华大学出版社