【背景】
在我们学过的查找方法中，在顺序表上进行的查找操作中，如果想查找某个关键字的记录，就是得从表头开始，逐个进行比较，直到找到关键字为止。到了后来我们学习了有序表地查找，利用折半查找的方法减少了查找的时间支出，提升了效率。但两种方法都有一个共同的特点，我们的目的都是为了找到关键字的下标i。就得通过关键字的相对位置进行查找。这两种查找方式为了查找结果，“比较”都是不可避免的，但这是否有必要？我们提出一种设想，有没有一种方法，能够直接通过关键字key得到要查找的记录内存的存储位置呢？答案是肯定的，于是引出今天的主角-散列表
【定义】
中学数学告诉我们，在函数的定义中，对于给定的自变量x，我们都有唯一确定的y与之对应，那么我们可否构造这样一个函数关系，将我们的数据构造某种特定的函数关系，让我们的自变量（存储位置x）与具体数值（因变量y）一一对应？这样我们的查找过程就可以直接通过该函数进行操作。
而散列表就是这样一种特殊的数据结构。定义如下：
散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f，使得每个关键字key对应一个存储位置f(key)。查找时，根据这个确定的对应关系找到给定值key的映射f(key)，若查找集合中存在这个记录，则必定在f(key)的位置上。
而这里，我们把这种对应关系f称为散列函数，又称哈希(hash)函数。按照这个思想，采用散列技术将记录存储在一块连续的存储空间中，这块连续存储空间，我们称之为散列表（Hash table）
【特点】
散列技术既是一种存储方法，也是一种查找方法。这种特点与函数与生俱来的性质一样，我们既可以通过key值推断出数据在表中的位置f(key)，又可以通过位置f(key)来判断key是否存在。
散列技术最适合的求解问题是查找与给定值相等的记录。（简化了比较步骤）
散列技术是利用散列函数f作为理论支撑，于是f的选取就称为了评判一个散列技术优劣的关键，而散列技术也有他的弊端，即f的选取在key值大范围内，会不可避免地产生冲突。
冲突：在现实生活中，或者在我们的数学学习生活中，我们会遇到x的取值不同，但y的取值是相同的，而我们如果按照这样的关系建立散列表，就会产生碰撞，\( 即：key1 \neq key2,但是却有 f(key1) = f(key2)\)。
我们称这种现象为冲突，并把key1,key2称为这个散列表的同义词。
【散列函数的构造法】
我们事先给出评价散列函数优劣的评判标准：
1、计算简单
2、散列地址分布均匀
第一点是顾名思义是为了减少计算机在计算散列函数时带来的时间开销。[从时间复杂度层面考虑]
第二点则是为了保证存储空间的有效利用。[从空间复杂度层面考虑]
在综合考虑这两种标准的基础上，本文列举几种常用的几种散列构造方法。
一、直接定址法：
如果我们要对下表中进行函数设计。我们设置一个长度为21的数组 a[21]
| 地址 | 年龄 | 人数 |
| 00 | 0 | 600万 |
| 01 | 1 | 500万 |
| 02 | 2 | 450万 |
| … | … | … |
| 20 | 20 | 1500万 |
表中以关键字(key)年龄直接作为地址存储位置，这样我们想查找年龄为20的人口分布，可以直接访问a[20]，即可得出它的数据。
此时散列函数为\(f(key) = key\)
而从下表分析：我们设置一个长度为21的数组 a[21]
| 地址 | 出生年份 | 人数 |
| 00 | 1980 | 1500万 |
| 01 | 1981 | 1600万 |
| … | … | … |
| 20 | 2000 | 800万 |
我们现在要统计的是80后出生年份的人口数，那么我们队出生年份这个关键字可以用年份减去1980来作为地址.那么我们访问第20号位置的元素即为2000年的人口信息。
此时f(key) = key – 1980
综合上述，我们可以取关键字的某个线性函数值作为散列地址，即：
\( f(key) = a \times key + b (a、b为常数)\)这样的散列函数优点是简单、均匀，也不会产生冲突，但问题是这需要事先知道关键字的分布情况，适合查找表较小且连续的情况，由于这样的限制，在现实应用中，并不常用
二、数字分析法
如果我们的关键字很长，（位数长）比如我们的手机号码是11位数的字符串，（180xxxx5671）,而现实中，电信运营商是这样定义的：我们的手机号码，前三位是接入号，对应不同运营商公司的子品牌，中间四位是HLR识别号，对应用户的归属地，而后4位才是真正的用户号，如下表所示
| 180xxxx1234 |
|
180xxxx2345 |
| 180xxxx3456 |
| 180xxxx4567 |
| 180xxxx5678 |
若用前一种方法（直接定址法），以手机号码作为关键字存储员工信息，那么我们从上述表中可知，员工的前7位数极有可能是相等的，而唯一的不同就是用户号，此时我们选取后4位作为散列地址作为key构造散列函数是一种选择。
而上述方法用抽象的定义可以定义为：抽取。即我们在数字分析法阶段，区别于直接定址法是多做了一步抽取的操作。
而抽取方法是使用关键字的来计算散列存储位置的方法，这在散列函数中是常常用到的手段。
综上所述，我们得知：
数字分析法通常适用于处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布较均匀，就可以考虑这个方法。
三、平方取中法
这个方法计算很简单，假定关键字是1234，那么它的平方就是1522756，再抽取中间的3位就是227，用作散列地址。在比如4321，它的平方就是18671041，取中间三位，671，也可以是710，用作散列地址。
平方取中法比较适合于不知道关键字的分布，而位数不是很大的情况。
四、折叠法
折叠法是将关键字从左到右分割成位数相等的几部分（ps.最后一部分位可以与前几部分不等长，但只能短一些），然后将这几部分叠加求和，取后几位作为散列地址；
如：9876543210,散列表长3位，我们将它分为四组987|654|321|0，然后将他们叠加求和987+654+321+0=1962,再求后三位得到散列地址为962.
有时，可能采取这样的方式还不能保证分布均匀，不妨从一端向另一端来回折叠后对齐相加。步入将987和321反转，再与654和0相加，编程789+654+123+0=1566，此时散列地址为566
折叠法事先不需要知道关键字的分布，适合关键字位数较多的情况。
五、除留余数法
除留余数法是最为常用的构造散列函数的方法，对于散列表常为m的散列函数公式为：
\( f(key) = key \% p (p \leq m)\)从上式可知，本方法的关键在于选择合适的p，p如果选择不好就容易产生同义词。
根据前人的经验我们得知，若散列表长度为m，通常p为小于或等长于m（最好接近于）的最小质数。
六、随机数法
随机数法是选取一个随机数，去关键字的随机函数值作为它的散列地址。也就是
\( f(key)=random(key)\)这里的randon是随机函数，当关键字长度不等时，采用这个方法构造散列函数是比较合适的。
【处理散列冲突的方法】
一、开放地址法
开放定址法就是一旦发生了冲突，就去寻找下一个空的散列地址，只要列表足够大，空的散列地址总能找到并将记录写入。
它的公式是：
\( f_i (key) = (f(key) + d_i) \% m (d_i = 1,2,3,\cdots,m-1)\)我们把这种解决冲突的开放定址法称为线性探测法。而上述公式称为一次/线性探测法。
采用一次线性探测法容易产生数据聚集，使得我们需要不断处理冲突，这样给我们的存入或者查找带来时间支出。
为了解决上述的问题，我们增加一个平方运算的操作。这样关键字就不会都聚集在某一块区域，我们称这样的方法为二次探测法。
公式如下：
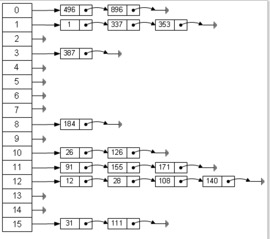
\( f_i = (f(key) + d_i) \% m (d_i = 1^2,-1^2,2^2,-2^2,\cdots,q^2,-q^2,q \leq \frac{m}{2})\)二、链地址法
链地址法是相对于第一种方法而提出的一种解决冲突的方法，其本质在于，我们再遇到冲突时无需另寻他径，只需要在原地增加链地址即可以解决冲突。
我们将所有关键字为同义词的记录存储在一个单链表中，我们称这种表为同义词子表，在散列表中只存储所有同义词子表的头指针。
【散列表构造/查找法源码实现】
以除留余数法+一次探测开放地址法为例
#define SUCCESS 1
#define UNSUCCESS 0
#define HASHSIZE 12
#define NULLKEY -32768
typedef struct
{
int *elem;
int count;
}Hashtable;
int m = 0;
/*
* 方法名：InitHashTable
* 作用：初始化散列表
* Author: WellLee
* 最后一次修改时间：2018年12月2日 19:28:04
*/
Status InitHashTable(Hashtable *H)
{
int i;
m = HASHSIZE;
H->count = m;
H->elem = (int *)malloc(m*sizeof(int));
for(i = 0; i < m; i++)
{
H->elem[i] = NULLKEY;
}
return OK;
}
/*
* 方法名：Hash
* 作用：哈希函数
* Author: WellLee
* 最后一次修改时间：2018年12月2日 19:28:04
*/
int hash(int key)
{
return key % m;
}
/*
* 方法名：InsertHash
* 作用：向哈希表中插入数据
* Author: WellLee
* 最后一次修改时间：2018年12月2日 19:28:04
*/
void InsertHash(HashTable *H,int key)
{
int addr = Hash(key);
while(H->elem[addr] != NULLKEY)
{
addr = addr+1 % m;
}
H->elem[addr] = key;
}
Status SearchHash(HashTable H, int key, int *addr)
{
*addr = Hash(key);
while(H.elem[*addr] != key)
{
*addr = (*addr + 1) % m;
if(H.elem[*addr] == NULLKEY || *addr = Hash(key))
{
return UNSUCCESS;
}
}
return SUCCESS;
}
【总结】
文章最后，我们对散列表查找的性能做一个简单分析，如果没有冲突，散列查找是我们本章介绍的所有查找中效率最高的，因为它的时间复杂度为O(1)，但在实际的应用中，冲突是不可避免的。于是给出散列查找的平均查找长度取决因素：
-
散列函数是否均匀
散列函数的好坏直接影响着出现冲突的频繁程度，不过，由于不同的散列函数对同一组的随机的关键字，产生冲突的可能性是相同的，因此我们可以不考虑它对平均查找长度的影响。
-
处理冲突的方法
相同的关键字、相同的散列函数，但处理冲突的方法不同，会使得平均查找长度不同。比如线性探测法处理冲突可能会产生堆积，显然就没有二次探测法好，而链地址法处理冲突不会产生冲突，因而具有更佳的平均查找性能。
-
散列表的装填因子
\(\begin{align} & 所谓的装填因子\alpha=填入表中的记录个数 / 散列表长度。\\ & \alpha 标志着散列表的装满程度。当填入表中的记录越多，产生冲突的可能性就越大。\\ & 也就是说，散列表的平均查找长度取决于装填因子，而不是取决于查找集合中的记录的个数。\end{align}\)不管记录个数 n有多大，我们总可以选择一个合适的装填因子以便将平均查找长度限定在一个范围以内，此时我们散列查找的时间复杂度就真的是O(1)了，为了做到这一点，通常我们都是将散列表的空间设置得比查找集合大，此时虽然是浪费了一定的空间，但换来的是查找效率的提升，总的来说，还是非常值得的。
【参考文献】
-
《大话数据结构》.程杰.清华大学出版社