【1.What】
自编码器（Autoencoder）是神经网络中的一种，经过训练后能尝试将输入复制到输出，其内部具有一个隐藏层h，可以产生编码(code)表示输入，该网络可以看作由两部分组成：
1、一个由函数\( h = f(x)\)表示的编码器
2、一个生成重构的解码器\(r = g(h)\)
其计算图表示如下所示：
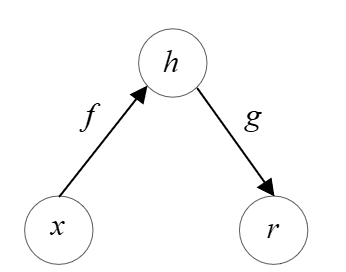
将网络输入复制到输出听起来没什么用处，但自编码器得核心思想不是关注解码器的输出，相反，如果通过在训练中自编码器对输入进行复制从而使得\( h \)获得更有用的特性，这是可行并符合实际应用的。
【2.欠完备自编码器】
在基础自编码器上，我们限制\( h \)的维度比\(x\)小，这种编码维度小于输入维度的自编码器称为欠完备(undercomplete)自编码器，学习欠完备的表示将强制自编码器捕获训练数据中最显著的特征。
其训练过程如下表示：
\( \mathrm{argmin}\{L(x, g(f(x)))\}\)
其中\(L\)是一个损失函数，衡量\(g(f(x))\)与\(x\)的差异。常用的有MSE。
notes:
1、当解码器是线性的且L是MSE，欠完备的自编码器会学习出与PCA相同的生成子空间，这种情况下，自编码器在训练过程中执行复制任务的同时还学习到了训练数据得主元子空间。
2、如果编码器和解码器被赋予过大的容量，自编码器会单纯地执行复制任务从而捕获不到任何有关数据分布的有用信息。
【3.正则自编码器】
欠完备自编码器在一定程度上能够捕获训练数据中的最显著特征，但当隐藏编码维度与输入维度相等或大于输入维度（过完备）时，线性解码器会单纯地将输入复制到输出而学不到任何数据分布的有用信息。
理想情况下，我们根据要建模数据分布的复杂性，选择合适的编码维度、解码器/编码器得容量就可以很好地训练任意架构的自编码器。如何选择这样的参数？这似乎也成为一个具有挑战性的问题。
正则自编码器提供另一种方法，它使用损失函数鼓励模型学习其它特性（除了单纯地将输入复制到输出），而不必限制是用浅层的编码器和解码器以及小的编码维度来限制模型容量。这些特性包括稀疏表示、表示的小导数以及对噪声或输入缺失的鲁棒性。即使模型容量大到足以学习一个无意义的恒等函数，非线性且过完备的正则自编码器仍然能够从数据中学到一些关于数据分布的有用信息。
【3.1.稀疏自编码器】
稀疏自编码器简单地再训练时结合编码层的稀疏误差\(\Omega{(h)}\)和重构误差，如下式表示：
\( \mathrm{argmin}\{L(x, g(f(x))) + \Omega{(h)}\}\)
其中：\(g(h)\)是解码器得输出，通常\(h\)是编码器的输出，即：\( h = f(x)\)
稀疏自编码器一般用于学习特征，以便用于像分类这样的任务，稀疏正则化的自编码器必须反映训练数据得独特统计特征，而不是简单地充当恒等函数，以这种方式训练，执行附带稀疏惩罚的复制任务可以学习到有用特征的模型。
【3.2.去噪自编码器】
除了向代价函数增加一个惩罚项，我们也可以通过改变重构误差来获得一个能学到有用信息的自编码器。
传统编码器训练如下：
\( \mathrm{argmin}\{L(x, g(f(x)))\}\)
如果模型被赋予过大的容量，\( L \)仅仅学到一个\( f \circ g\)的恒等函数。
与此相反，去噪自编码器（denoising autoencoder, DAE）训练：
\(\mathrm{argmin}\{L(x), g(f(\widetilde{x}))\}\)
其中\(\widetilde{x}\)是被某种噪声损坏的\( x \)副本，因此去噪自编码器必须撤销这些损坏，而不是简单地复制输入。
【3.3.惩罚导数作为正则】
另一正则化自编码得策略是是用一个类似于稀疏自编码器中的惩罚项\( \Omega\)
\(\mathrm{L(x, g(f(x))) + \Omega{(h, x)}}\)
但是\(\Omega\)的形式不同:
\(\begin{align} \Omega(h, x) = \lambda \sum_i ||\bigtriangledown_x h_i||^2 \end{align}\)
这强迫模型学习一个在\( x \)变化小时目标也没有太大变化的函数，因为这个损失只对训练数据是用，它迫使自编码器学习可以反映训练数据分布信息的特征。
这样的正则化自编码器被称为收缩自编码器（Contractive autoencoder, CAE）。
【4.随机编码器和解码器】
自编码器本质上是一个前馈神经网络，可以是用与传统前馈网络相同的损失函数和输出单元。
设计前馈神经网络的输出单元和损失函数普遍的策略是定义一个输入分布\( p(y|x)\)并最小化负对数似然\( -\mathrm{log}p(y|x)\)。在这种情况下:\(y\)是关于目标的向量（如类标）。
在自编码器中，\(x\)既是输入也是目标，然而我们仍然可以使用与之前相同的架构，给定一个隐藏编码\( h\),我们认为解码器提供了一个条件分布\( p_{\mathrm{model}}(x|h)\)。接着我们根据最小化\(-\mathrm{log}p_{\mathrm{decode}}(x|h)\)来训练自编码器，损失函数视\( p_{decoder}\)的形式而定。就传统的前馈神经网络来说，如果\(x\)是实值，那么我们通常是用线性输出单元参数化高斯分布的均值。再这种情况下，负对数似然对应均方误差准则，类似的，二值\(x\)对于一个Bernoulli分布，其参数由sigmoid输出单元确定，而离散的\(x\)对应softmax分布，以此类推，再给定h的情况下，为了便于计算概率分布，输出变量通常被视为条件独立的，但一些技术（如混合密度输出）可以解决输出相关建模。
为了更彻底地与我们之前了解到的前馈网络相区别，我们可以将编码函数（encoding function）\( f(x)\)的概念推广到编码分布（encoding distribution）\( p_{\mathrm{encoder}}(h|x)\),如下图所示：
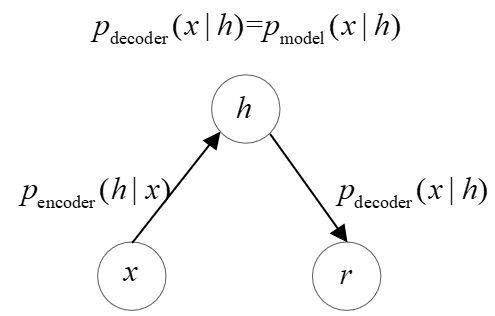
通常情况下，编码器和解码器得分布没有必要是与唯一联合分布\(p_{\mathrm{model}}(x, h)\)相容的条件分布。在保证足够的容量和样本情况下，将编码器和解码器作为去噪自编码器训练，能够使他们渐近地相容。
【5.表示能力、 层的大小和深度】
自编码器通常只有单层的编解码器，但这不是必然的，实际上深度编码器和解码器能提供更多优势。它也属于前馈神经网络，所以也具有与前馈神经网络一样的优势，编码器和解码器两个部分都能各自从深度结构中取得好处。
万能近似定理保证至少有一层隐藏层且隐藏单元足够多的前馈神经网络能够以任意精度拟合任意函数（在很大范围里），这时非平凡深度（至少有一层隐藏层）得一个主要优点。这意味着具有单隐藏层的自编码器再数据域内能表示任意近似数据的恒等函数。但是，从输入到编码的映射时浅层的，这意味着我们不能任意添加约束，比如约束编码系数。深度自编码器（编码器至少包含一层隐藏层）再给定足够多的的隐藏单元的情况下，能以任何精度近似任何从输入到编码的映射。。
深度可以指数地降低表示某些函数的计算成本。也能指数地减少学习一些函数的训练数据量。而深度自编码器能比相应的浅层或线性自编码器产生更好地压缩效率。
训练深度自编码器的策略是训练一堆浅层的自编码器来贪心地与训练相应得深度架构，所以即使最终目标是训练深度自编码器，我们也经常会遇到浅层自编码器。
【参考文献】
-
Ian Goodfellow, Yoshua Bengio. Aaron Courville.Deep Learning[M].2017(08):306-319