极限:
“极限”是数学中的分支——微积分的基础概念,广义的“极限”是指“无限靠近而永远不能到达”的意思。数学中的“极限”指:某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”(“永远不能够等于A,但是取等于A‘已经足够取得高精度计算结果)的过程中,此变量的变化,被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”(当然也可以用其他符号表示)。
思维导图:
\(极限\begin{cases} 数列极限\begin{cases} 定义 \\ 性质\begin{cases} 唯一性 \\ 保号性 \\ 有界性 \end{cases} \end{cases} \\ 函数极限\begin{cases} 自变量趋于有限值\begin{cases}定义 \\ 性质\begin{cases} 唯一性 \\ 保号性 \end{cases}\end{cases} \\ 自变量趋于无穷大\begin{cases}定义\\性质\begin{cases}唯一性 \\ 保号性\end{cases}\end{cases}\end{cases} \\无穷大/无穷小\begin{cases}无穷小\begin{cases} 定义 \\ 性质\end{cases} \\ 无穷大\begin{cases}定义 \\ 性质\end{cases}\end{cases} \end{cases}\)一、数列极限:
定义:
\(\begin{align}&设{x_n}为一数列,如果存在常数A,对于任意给定的正数\epsilon(不论它多么小),\\ &总存在正整数N,使得当n>N时, 不等式\\& |x_n -a| < \epsilon \\&都成立,那么就称常数A是数列{x_n}的极限,或者称数列{x_n}收敛于A,记为\\& \lim_{n \to \infty}x_n = A \\&或 \\& x_n \to a(n \to \infty)\end{align}\)
引论:
\(\begin{align} & 设数列{a_n},常数A \\ &若\forall\epsilon>0,\exists N>0,当n>N时\\ & |a_n -A| < \epsilon \\& 则有:\lim_{n \to \infty }|a_n| = A\end{align}\)性质:
唯一性: \(\begin{align} \lim_{n \to \infty}a_n = A,\lim_{n \to \infty}a_n = B \rightarrow A=B \end{align}\)
利用反证法证明:\(\begin{align} &设A >B \\&取 \epsilon = \frac{a-b}{2} > 0 \\& 因为\lim_{n \to \infty}a_n = A 因此 N > 0,当n > N1时, |a_n – A| < \frac{A-B}{2} \\& \frac{A+B}{2} < a_n < \frac{3A-B}{2} (*) \\&而\lim_{n \to \infty}a_n = B 同理也有 \frac{3B-A}{2} < a_n < \frac{A+B}{2}(**)\\&取N=max\{N1,N2\},当n > N时,(*)(**)都成立 \\ & 但通过观察,这样的N值并不存在,故假设矛盾,同理证得A < B同样矛盾。\\&故 A = B \end{align}\)
保号性: \(\begin{align} \lim_{n \to \infty}a_n = A\begin{cases}A>0 \\ A<0\end{cases} \rightarrow \exists N>0,当 n >N时,a_n\begin{cases}a_n > 0 \\ a_n < 0\end{cases} \end{align}\)
证明:\( \begin{align} &①假设A>0 \\ &取\epsilon = \frac{A}{2} > 0 \\&因为:\lim_{n \to \infty}a_n = A \\& 所以: \exists N>0 当n > N时,|a_n – A| < \frac{A}{2} \Rightarrow a_n > \frac{A}{2} \Rightarrow a_n > 0 \\&②假设A < 0 \\&取\epsilon = -\frac{A}{2} > 0 \\& 同理 \exists N >0 |a_n -A| < -\frac{A}{2} \Rightarrow a_n < \frac{A}{2} \Rightarrow a_n < 0 \end{align}\)
有界性: \( \begin{align} \lim_{n \to \infty}a_n = A,则\exists M>0,使得|a_n| \leq M \end{align}\)
二、函数极限
1.自变量趋于有限值
Notes:
- \(x \to a \rightarrow x \neq a\)
-
\(x \to a\begin{cases}x \to a^- \\ x \to a^+\end{cases}\)
-
\(0 < |x-a| < \delta \Rightarrow x \subseteq (a-\delta,a) \cup (a, a+\delta)\)
定义:
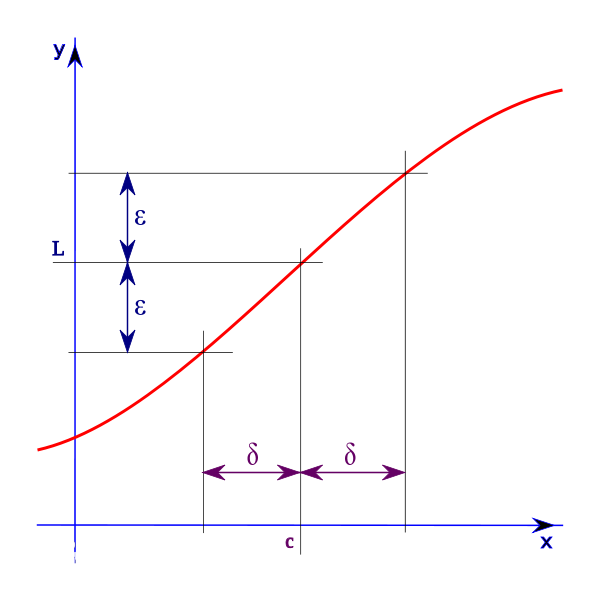
\(\begin{align}&y=f(x)在x=a,去心领域内有定义\\&若\forall \epsilon > 0 , \exists \delta >0,当 0 <|x-a| < \delta时 \\ &|f(x)-A|< \epsilon \\ &称 \lim_{x \to a}f(x) = A \end{align}\)
Notes:
-
\(\begin{align} \lim_{x \to a}f(x)与f(a)无关。例子:\lim_{x \to 1}\frac{x^2-1}{x-1}=\lim_{x \to 1}(x+1) = 2\end{align}\)
-
\(\begin{align} &若\forall \epsilon > 0,\exists \delta > 0,当x\subseteq(a-\delta,a)时\\ &|f(x)-A| < \epsilon \\&称A为f(x)在x=a处的左极限,记f(a-0) = A \end{align}\)
-
\(\begin{align} &若\forall \epsilon > 0,\exists \delta > 0,当x\subseteq(a,a+\delta)时\\ &|f(x) – B| <\epsilon \\&称B为f(x)在x=a处的右极限,记f(a+0) = B\end{align}\)
- \(\begin{align}\lim_{x \to a}f(x) \exists \Leftrightarrow f(a-0) ,f(a+0)存在且相等\end{align}\)
2.自变量趋于无穷大
Notes:
- \( \begin{align} &若\forall \epsilon > 0,\exists X > 0 ,当 x > X时 \\ &有 |f(x) – A| < \epsilon \\ &则有: \lim_{x \to +\infty}f(x) = A \end{align}\)
- \( \begin{align} &若\forall \epsilon > 0,\exists X > 0 ,当x < -X时 \\ &有 |f(x)-A| < \epsilon \\ &则有: \lim_{x \to -\infty}f(x) = A \end{align}\)
- \(\begin{align} &若\forall \epsilon > 0,\exists X>0,当|x| > X时 \\ &有|f(x) -A| < \epsilon \\&则有: \lim_{x \to \infty}f(x) = A\end{align}\)
性质:(两种情况都成立,无论是自变量趋于有限值还是无穷大)
唯一性:
\(\lim f(x) = A,\lim f(x) = B \Leftrightarrow A = B\)
保号性:
\(\begin{align} & \lim_{x \to a}f(x) = A\begin{cases} A >0 \\ A <0 \end{cases} \\ & 则\exists \delta > 0,当0 < |x – A| < \delta 时 \\ & f(x)\begin{cases} f(x) > 0 \\ f(x) < 0 \end{cases} \end{align}\)证明:
\(\begin{align}&假设A > 0 \\&取 \epsilon = \frac{A}{2} > 0,当0 <|x-A| < \delta时 \\& |f(x) – A| < \frac{A}{2} \Rightarrow f(x) > A – \frac{A}{2} = \frac{A}{2} > 0 \\&同理可证当A<0时的条件成立\end{align}\)
三、无穷小与无穷大
1、无穷小
定义
\(\begin{align} \lim_{x \to a} \alpha (x) = 0 称 \alpha (x)在当x \to a 时为无穷小\end{align}\)
简单来说,以零为界限就称为无穷小。
Notes
零是无穷小,但无穷小不一定是零
非零函数是否无穷小与它的自变量趋势有关
例如:\(\begin{align} &\alpha = 3(x-1)^2 \\ &3(x-1)^2当x \to 1时,它为无穷小 \\& 3(x-1)^2当x \to 2时,它不为无穷小 \end{align}\)
性质
①\( \alpha \to 0,\beta \to 0 \Rightarrow \alpha \pm \beta \rightarrow 0 \)
证明: \(\begin{align}&因为\lim_{x \to a}\alpha = 0; \lim_{x \to a}\beta = 0 \\& \forall \epsilon > 0,\exists \delta_1 > 0,当0 <|x-a| < \delta_1时 \\& 有:|\alpha – 0 | < \epsilon (*) \\ & \exists \delta_2 > 0 当 0 < |x-a| < \delta_2时 \\&有:|\beta – 0| < \epsilon(**)\\&取\delta = min\{\delta_1,\delta_2\},当0<|x-a|<\delta时,\\& (**)和(*)都成立\\&当0 < |x-a| < \delta时 \\& |(\alpha \pm \beta) – 0| \leq |\alpha| + |\beta| = |\alpha – 0| +|\beta-0| < 2 \epsilon \\& 即|(\alpha \pm \beta) -0| < 2\epsilon (本质上此处的\epsilon为任意值) \\& 所以:\lim_{x \to a}(\alpha \pm \beta)=0 \end{align}\)
②\( \alpha \to 0,\beta \to 0 \Rightarrow \alpha \beta \rightarrow 0 \)
证明: \(\begin{align}&设\lim_{x \to a}\alpha = 0,\lim_{x \to a}\beta = 0 \\&取\epsilon_0 =1,\exists \delta_1>0,当0 <|x-a| <\delta_1时 \\& |\alpha – 0|<1,即|\alpha| < 1(*) \\ &\forall \epsilon > 0,\exists \delta_2 > 0 当 0<|x-a|<\delta_2时 \\& |\beta – 0| < \epsilon (**) \\ &取\delta = min \{\delta_1,\delta_2\}时\\&(*)(**)成立\\&|\alpha \beta – 0| = |\alpha||\beta| < \epsilon \\&所以\lim_{x \to a}\alpha \beta = 0 \\& 故称:有限个无穷小相乘仍等于无穷小\end{align}\)
③\(|\alpha| \leq M,\beta \to 0 \Rightarrow \alpha \beta \rightarrow 0 \)
证明: \(\begin{align}&因为\lim_{x \to a}\beta = 0 \\& \forall \epsilon > 0,\exists \delta > 0,当0<|x-a|<\epsilon时 \\&|\beta| < \epsilon \\&当 0 <|x-a| < \epsilon时 \\& |\alpha \beta -0| = |\alpha| \cdot |\beta – 0| = M\epsilon \\& 所以: \lim_{x \to a}\alpha \beta =0 \\&故称:有界函数与无穷小的函数仍等于无穷小\end{align}\)
④ \(\begin{align}\lim_{x \to a}f(x) = A \Leftrightarrow f(x) = A + \alpha,其中 \alpha \to 0 (x \to a)\end{align}\)
证明: \(\begin{align}&"\Rightarrow"必要性证明 \\& 设 \lim_{x \to a}f(x) = A \\& \forall \epsilon>0,\exists \delta >0,当0<|x -a| < \epsilon时\\&|f(x)-a| < \epsilon \\& 令 \alpha=f(x) – A \Rightarrow f(x)=A+\alpha \\&因为\forall \epsilon>0,\exists \delta>0,当0<|x-a|<\delta时\\&|\alpha| < \epsilon或称|\alpha -0 |< \epsilon \\&所以:\lim_{x \to a}\alpha = 0 \\ & "\Leftarrow"充分性证明 \\&设f(x) = A + \alpha,\alpha \to 0(x \to a) \\& \forall \epsilon, \exists \delta >0,当0 <|x-a| < \delta时\\&|\alpha – 0|<\epsilon \\&即|f(x)-A| < \epsilon \\&所以:\lim_{x \to a}f(x) = A \end{align}\)
2、无穷大
关于无穷大的定义与性质可以用一句话概括:无穷大即无穷小的倒数,欲证明其定义与性质只需证明无穷小的倒数即可
四、参考文献
-
《高等数学》第七版-上册 同济大学数学系 编
屌爆了,差点没发现是个人网站🤯