【机器学习】神经网络中前向传播，反向传播公式推导

【背景】

        从深入了解了当前流行机器学习算法之后，我们可以总结出，一个机器学习算法其实只有两部分：

1、Model <-> Hypothesis <-> 从输入特征\(x\)预测输出\(y\)的函数\(h(x)\)

2、Costfunction  <-> Objectfuntion <-> 目标函数/损失函数（虽然在深度学习领域这两个函数定义还有所不同，但从机器学习领域这两个函数我们不做过多的分界）

        知道机器学习这两个关键部分，我们要介绍一个算法（机器学习）， 只需要列出这两个函数就可以了。

        机器学习的的本质是利用优化算法（Grandient Descent / Grandient Ascent）来针对目标函数/损失函数进行优化，从而能找到一个局部最优值。而这些局部最优值（模型参数）就组成了我们的Model.

        在机器学习中，算法往往不是关键，真正的关键之处在于特征选取，选取特征需要我们人类对问题的深刻理解，经验、思考。（What 's the Model we need? ）即我们需要的Model是一个Linear Regression问题解法，Or Logist Regression even more?

        在机器学习有这么一个算法：深度学习。其一个优势就是它能自动学习到应该提取什么特征，从而使算法不那么依赖人类，这是神经网络暴露在当今人类视野中的一个方面，但也是让人感觉到一股玄学之所在面。

【神经网络基础】

计算机中的神经网络可以说是仿真人脑的神经单元的应用。与初中生物学习的神经单元结构类似。两者对比图如下所示：

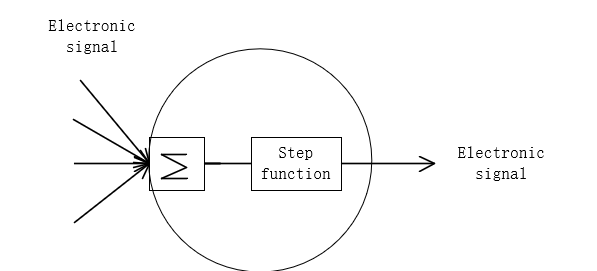
        感知机和神经元本质上是一样的，只不过我们说感知机的时候，它的激活函数是阶跃函数，当我们说神经元时，激活函数往往选择为sigmoid函数或tanh函数。计算某个神经元输出的方法和计算一个感知机的输出是一样的。假设神经元的输入是向量\( \vec x \)，权重向量是\( \vec \omega\)(其中偏置项是\( \omega_0\))，激活函数是sigmoid函数，则其输出y:

\(\begin{align} y = sigmoid(\vec \omega^T \cdot \vec x ) && (1) \end{align}\)

其中sigmoid函数定义如下：

\(\begin{align}sigmoid(x) = \frac{1}{1 + e^{-x}} \end{align}\)

将sigmoid函数代入式(1):

\( y = \frac{1}{ 1 + e^{-{\vec \omega}^T \cdot \vec x}}\)

sigmoid函数是一个非线性函数，其值域是(0, 1)。函数图像如下图所示：

sigmoid函数的导数是:

\( y^{'} = y(1 – y)\)

【神经网络架构】

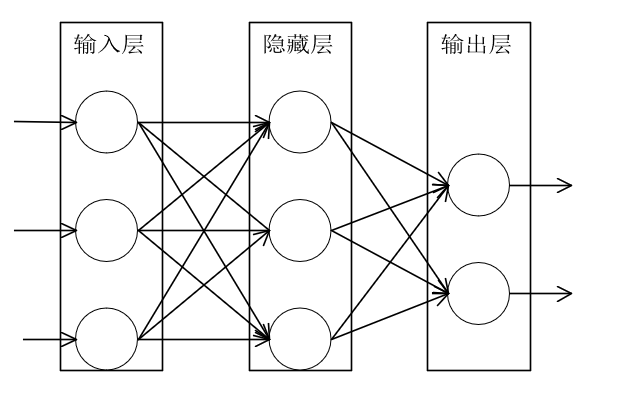
        神经网络就是按照一定规则连接起来的多个神经元，以下图全连接神经网络(Full connected, FC)为例对神经网络的架构进行说明。

• 神经元按层来布局，最左边的层叫做输入层，负责接收输入数据，最右边的层叫做输出层，我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的

• 同一层神经元之间没有连接

• 第N层的每个神经元和第N-1层的所有神经元相连（Full Conneted），第N-1层神经元的输出就是第N层神经元的输入求和（summation）.

• 每个连接都有一个权值（Weight）

【全连接网络前向传播】

        从全局上看，神经网络实际上就是一个输入向量\( \vec x\)到输出向量\( \vec y\) 的函数，即：

\(\vec y = f_{model}(\vec x)\)

        以神经元为单位上来看，欲计算整个神经网络模型\( f_{model}\)，需要利用输入向量\(\vec x \)来求出下一层隐藏层（n+1）中每一个神经元的输出值，然后再用这些输出值作为再下一层隐藏层(n+2)层的输入求出该层的每一个神经元输出值，依此递推直到求出输出层的输出值。即为我们的输出向量\( \vec y\)

举例说明：

以上图全连接网络的前向传播进行介绍。我们人为地给神经网络编号。以及进行数学符号量化。

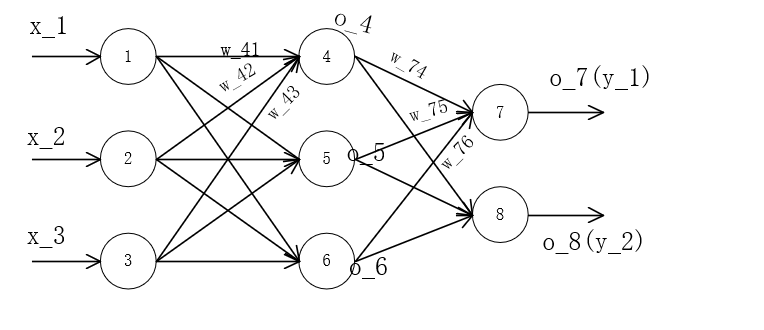
（笔者用VISIO制图，_后的数字代表下标如w_41代表\( \omega_{41}\))

结构说明：

        上图中我们以单个数字对神经元进行编号，如图，1，2，3号神经元是输入层的三个节点，4，5，6为隐藏层的三个节点，7，8为输出层的两个节点。全神经网络的性质显而易见：每个节点都与上一层的节点进行连接，如节点4同时与1，2，3节点进行连接。其连接线路(权重)为\(\omega_{41}, \omega_{42}, \omega_{43}\)。那么欲求节点4的输出\(o_4\)。我们用到如下式子。（输入层的输出即为\( \vec x\)）

为了使式子更直观，我们将式子向量化表示：于是得出式子：

\( o_4 = sigmoid({\vec w}^T \cdot \vec x)\)

从这个式子可以延伸出两种情况：

1、若全连接网络中只有一层隐藏层，则:

\(\begin{cases}o_{n}^{hidden} = sigmoid({\vec w}  ^T \cdot  \vec x) & (1) \\ \vec y = sigmoid({\vec w}^T \cdot {\vec o_{n-1}^{hidden}}) &(2)\end{cases}\)

2、若全连接网络中有多层隐藏层，则：

\(\begin{cases} o_{n}^{h_1} = sigmoid({\vec w_{1}} ^ T \cdot \vec x) & m == 1 \\ o_{n}^{h_m}  = sigmoid({\vec w_{m}}^T \cdot \vec o_{m}) & m > 1 \\ \vec y = sigmoid({\vec w_{last}}^T \cdot \vec o_{last}) & m == last+1\end{cases}\)

这两条式子则为神经网络的前向传播公式。

因为神经网络的特殊性质，我们知道，神经元的参数传递很大程度可以递归求解。给我们计算机编程带来了便利性。

【全连接网络反向传播】

        神经网络的训练就是需要知道一个神经网络的每个连接上的权值是如何知道的，我们可以说神经网络就是一个模型，那么这些权值就是模型中的参数，也就是模型要学习的东西，然而，一个神经网络的连接方式、网络的层数、每层的节点数这些参数，则不是模型学习出来的，而是人为事先设置的，对于这些认为设置的参数，我们称之为超参数（Hyper-Parameters）。而得出模型参数的方法（神经网络的训练算法）就是我们接下来推导的反向传播算法。前后结合，我们还是利用前向传播中的全连接网络进行公式推导。结合前文，我们使用监督学习为例来解释。并且图中每个神经元的激活函数为sigmoid函数。而不同的激活函数计算公式不同。！！！

我们假设每个训练样本为\((\vec x, \vec t)\),其中向量\(\vec x\)是训练样本的特征,而\(\vec t\)是样本的目标值。

一个反向传播算法流程基本如下：

1、我们使用前向传播算法，用样本的特征\(\vec x\),计算出每个隐藏层节点的输出\(o_i\), 以及输出层每个节点的输出\(y_i\).

2、我们按照下面公式计算出每个节点的误差项\(\delta_i\):

2.1、那么对于输出层节点\( i\):

\(\begin{align}\delta_i = y_i(1 – y_i)(t_i – y_i) &&(式1)\end{align}\)

        其中，\(\delta_i\)是节点\(i\)的误差项，\(y_i\)是节点\( i\)的输出项，\(t_i\)是样本对于节点\(i\)的目标值。举个例子，根据上图，对于输出层节点7来说。它的输出值为\(y_1\)，而样本的目标值是\( t_1\)，带入上面的公式得到节点7的误差项\(\delta_7\)应该是：

\( \delta_7 = y_1(1-y_1)(t_1 – y_1)\)

2.2、对于隐藏层节点，

\(\begin{align}\delta_i = a_i(1-a_i)\sum_{k \in outputs} w_{ki} \delta_k  &&(式2)\end{align}\)

        其中，\(\begin{align}a_i\end{align}\)是节点\(\begin{align}i\end{align}\)的输出值，\(\begin{align}w_{ki}\end{align}\)是节点\(\begin{align}i \end{align}\)到它的下一层节点\(\begin{align}k\end{align}\)的连接权重，\(\begin{align}\delta_k\end{align}\)是节点\(\begin{align}i\end{align}\)的下一层节点\(\begin{align}k\end{align}\)的误差项，例如对于隐藏层节点4来说，计算方法如下：

\(\begin{align} \delta_4 = a_4(1-a_4)\sum_{i \in 4th outputs} w_{4i} \delta_4\end{align}\)

3、最后，更新每个连接上的权值：

 \( \begin{align}w_{ji} \leftarrow w_{ji} + \eta \delta_j x_{ji} &&式(3)\end{align}\)

        其中， \(w_{ji}\)是节点 \(i\)到节点 \(j\)的权重， \(\eta\)是学习速率的常数（超参数）, \(\delta_j\)是节点 \(j\)的误差项， \(x_{ji}\)是节点 \(i\)传递给节点 \(j\)的输入，例如，权重 \(w_{84}\)的更新方法如下：

 \(w_{84} \leftarrow w_{84} + \eta \delta_8 a_4\)

        从反向传播的计算过程中，我们直到，这个过程是通过正向传播的结果逆向利用梯度求导的一个流程。故名反向传播。其本质还是利用之前提及的梯度上升/下降进行优化 \(\vec w\) 而得出的局部最优解。

下文，我们针对本节提及的三条式子进行推导。

【全连接网络反向传播关键公式推导】

反向传播算法是链式求导法则的应用。

按照机器学习的通用套路，我们先确定神经网络的目标函数，然后用随机梯度下降优化算法取求目标函数最小值时的参数值。

我们取网络所有输出层节点的误差平方和作为目标函数：

\(\begin{align} E_d \equiv \frac{1}{2} \sum_{i \in outputs}(t_i – y_ i)^2\end{align}\)

其中, \(E_d\)表示样本d的误差。

接着，我们对目标函数用随机梯度下降算法对目标函数进行优化：

 \(w_{ji} = w_{ji} – \eta \frac{\partial E_d}{ \partial w_{ji}}\)

我们看图：

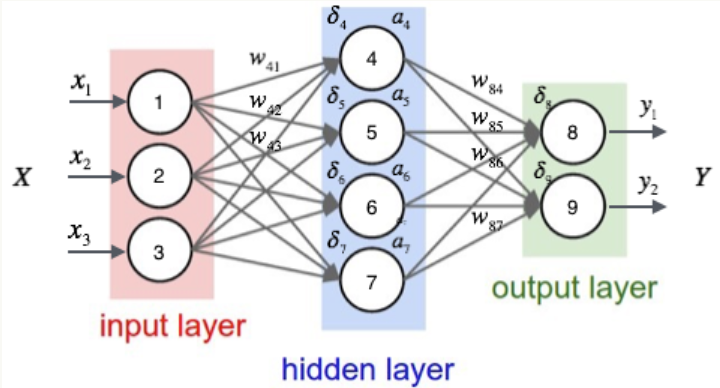
在图中我们得知\( w_{ji}\)仅能通过影响节点\(\begin{align} j\end{align}\)的输入值影响网络的其他部分，在此我们设\(\begin{align}net_j \end{align}\)是节点\(\begin{align} j\end{align}\)的加权输入，即：

\(\begin{align}net = & \vec{w_j} \cdot \vec{x_j} \\ = & \sum_{i}w_{ji}x_{ji} \end{align}\)

\(\begin{align}E_d \end{align}\)是\(\begin{align} net_j\end{align}\)的函数，\(\begin{align} net_j\end{align}\)是\(\begin{align}w_{ji} \end{align}\)的函数，根据链式求导法则，可以得到：

\(\begin{align}\frac{\partial E_d}{\partial w_{ji}} &= \frac{\partial E_d}{\partial net_j} \frac{\partial net_j}{\partial w_{ji}} \\ &=\frac{\partial E_d}{\partial net_j} \frac{\partial{\sum_i w_{ji}x_{ji}}}{\partial w_{ji}} \\ &= \frac{\partial E_d}{\partial net_j} x_{ji}\end{align}\)

化简后的结果中\(\begin{align} x_{ji}\end{align}\)是节点\(\begin{align} i\end{align}\)传递给节点的值，对于\(\begin{align}j\end{align}\)是输入值，对于\(\begin{align} i\end{align}\)是输出值。

而对于\(\begin{align} \frac{\partial E_d}{\partial net_j}\end{align}\)的推导，需要区分输出层和隐藏层两种情况。

case 1、输出层权值训练

对于输出层，\(\begin{align} net_j\end{align}\)仅能通过节点\(\begin{align}j\end{align}\)的输入值\(\begin{align}y_j\end{align}\)来影响网络的其他部分，也就是说\(\begin{align} E_d\end{align}\)是\(\begin{align} y_j\end{align}\)的函数，而\(\begin{align}y_j\end{align}\)是\(\begin{align}net_j\end{align}\)的函数，其中\(\begin{align}y_j = sigmoid(net_j) \end{align}\)。所以我们再次利用链式求导法则得出：

\(\begin{align}\frac{\partial E_d}{\partial net_j} = \frac{\partial E_d}{\partial y_j} \frac{\partial y_j}{\partial net_j}\end{align}\)

对于\(\begin{align} \frac{\partial E_d}{\partial y_j}\end{align}\):

\(\begin{align}\frac{\partial E_d}{\partial y_j} &=\frac{\partial}{\partial y_j} \frac{1}{2} \sum_{i \in outputs} (t_i – y_i) ^2 \\ &=\frac{\partial}{\partial y_j}\frac{1}{2}(t_j -y_j)^2 \\&=-(t_j – y_j) \end{align}\)

对于\(\begin{align}\frac{\partial y_j}{\partial net_j}\end{align}\)：

\(\begin{align}\frac{\partial y_j}{ \partial net_j} &= \frac{\partial sigmoid(net_j)}{\partial net_j} \\ &=y_j(1-y_j)\end{align}\)

将上述推导结果代入，得：

\(\begin{align}\frac{\partial E_d}{\partial net_j} = -(t_j – y_j)y_j(1-y_J)\end{align}\)

令\(\begin{align} \delta_j = -\frac{\partial E_d}{\partial net_j}\end{align}\)，也就是一个节点的误差项\(\begin{align} \delta \end{align}\)是网络误差对这个节点输入的偏导数的相反数，带入上式，得：

\(\begin{align} \delta_j = (t_j – y_j)y_j(1-y_j) &&（式1）\end{align}\) 

将上述推导代入SGD（随机梯度下降公式），得：

\(\begin{align} w_{ji} &= \leftarrow w_{ji} – \eta \frac{\partial E_d}{\partial w_{ji}} \\ &=w_{ji} + \eta (t_j – y_j)y_j(1-y_j)x_{ji} \\&=w_{ji} +\eta \delta_j x_{ji} & （式2）\end{align}\)

case2、对于隐藏层：

我们事先定义j的所有直接下游节点集合\(\begin{align} D(j) \end{align}\)，下游节点是指与节点\(\begin{align}j\end{align}\)的输出层直接相邻的节点。这样我们根据图解可知。\(\begin{align} net_j\end{align}\)只能通过影响\(\begin{align} D(j)\end{align}\)再影响\(\begin{align} E_d\end{align}\)。设\(\begin{align} net_k\end{align}\)是节点\(\begin{align} j\end{align}\)的下游节点的输入，则\(\begin{align}E_d\end{align}\)是\(\begin{align}net_k\end{align}\)的函数，而\(\begin{align}net_k\end{align}\)是\(\begin{align} net_j\end{align}\)的函数。而\(\begin{align}net_k\end{align}\)有多个，我们应用全导数公式，做出下列推导。

\(\begin{align}\frac{E_d}{net_j}&=\sum_{k \in D(j)}\frac{\partial E_d}{\partial net_k} \frac{\partial E_d}{\partial net_k} \\&=\sum_{k \in D(j)} -\delta \frac{\partial net_k}{\partial net_j} \\&=\sum_{k \in D(j)} -\delta_k \frac{\partial net_k}{\partial a_j} \frac{\partial a_j}{\partial net_j} \\&=\sum_{k \in D(j)} \delta_k w_{kj} \frac{\partial a_j}{\partial net_j} \\&=\sum_{k \in D(j)} -\delta w_{kj} a_j(1-a_j) \\&= -a_j(1-a_j)\sum_{k \in D(j)} \delta_k w_{kj}\end{align}\)

同样\(\begin{align} \delta_j = -\frac{\partial E_d}{\partial net_j}\end{align}\)，带入上式：

\(\begin{align} \delta_j = a_j(1-a_j)\sum_{k \in D(j)} \delta_k w_{kj} &&（式3）\end{align}\)

【总结】

        我们利用数学原理对神经网络进行了一次推导，但计算机对于真正意义上的仿真还存在一定的距离。但要真正踏入深度学习领域的大门，还有很长的路子要走。

【参考文献】

• 零基础入门深度学习