【算法设计与分析】概述（一）—<算法概念>

【由计算机求解引入的算法】

by N.Wirth

【问题引入】 

     在本科（计算机科班）学习中，周围很多同学都被C语言劝退在门槛之外，我想很大原因是许多同学缺乏现实求解与计算机求解相联系的能力。下图是Boss在硕士课堂上引入算法概念中的一张联系图。

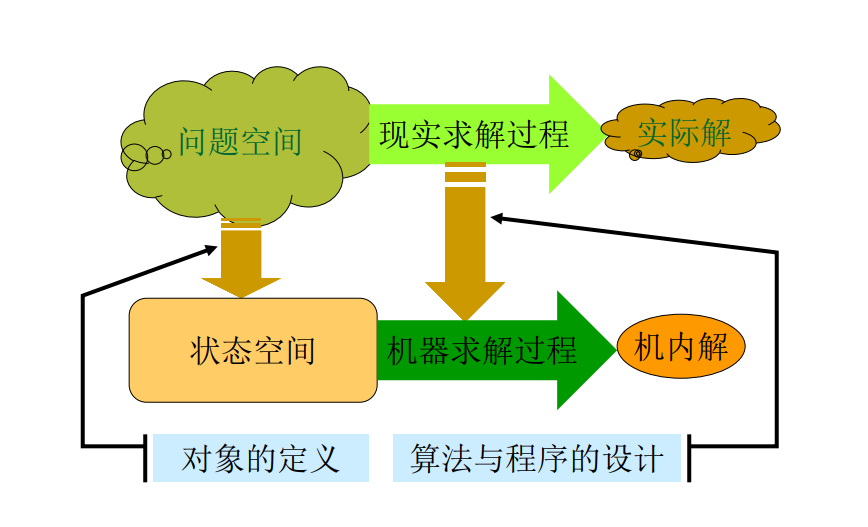
从图中我们作为程序员只需关注两个点：

1、实际问题空间与状态空间的转换

2、现实求解过程与机器求解过程的转换

而这两个点则分别对应：

1、现实问题空间状态、数据、对象的建模（定义）—数据结构定义

2、算法/程序设计

ps.篇幅有限，在此默认读者都具备了数据结构的知识。

【计算机求解过程】

形象化的求解过程入下图：

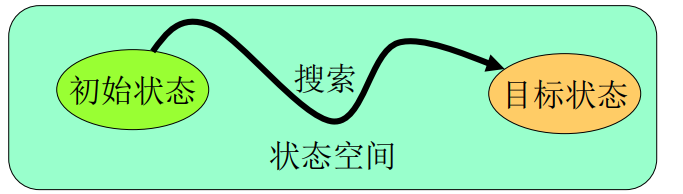
求解的过程可以看作：问题在状态空间从初始状态出发搜索目标状态（解所处于的状态）的过程。

从数学上定义如下：

问题初态定义为:\(S_0 \)

问题终态定义为:\(S_n\)

搜索过程如下：

\(S_0 \Rightarrow S_1 \Rightarrow \cdots \Rightarrow S_n\).

或:

\( \phi(S_0) \Rightarrow \varphi(S_n)\)

其中：

\(\phi\)称为初始条件

\( \varphi \)称为终止条件

更复杂的搜索如下图所示：

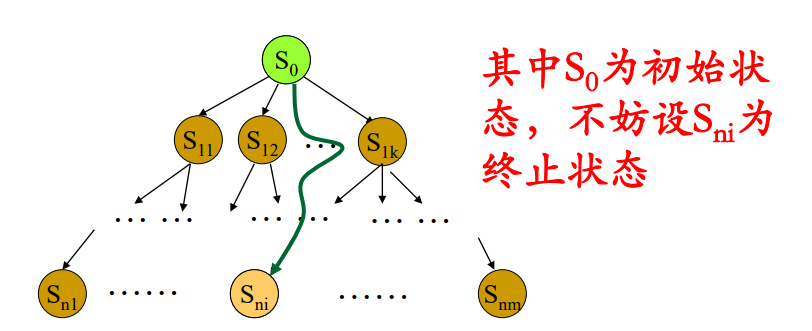
问题的求解就是通过搜索，找出一条从初始状态\(S_0\)到终止状态\(S_{ni}\)的路径（Path）。

而现实中有许多问题的求解并非只有一条路径，在此定义这些可行解集合为解空间。

而诸如一些动态规划、回溯求解的解空间我们也根据需要选出一条或者多条路径作为问题的最优解。

【计算机程序】

计算机要对现实问题求解，正如上文所说要做两件事情。

1、数据结构

2、算法设计

而这两件事都是由计算机程序来承担。

程序送计算机内进行信息处理的一种逐步描述，它具有：

• 有穷性：是由某种程序设计语言的若干条命令组成的
  有穷序列

• 确定性：每条命令的意义都是确定的；

• 零或多个输入：具有零个或多个输入

• 输出：产生若干个输出

程序的执行可能终止也可能不终止

【算法引入】

在很多国外的大学数据结构与算法设计是一门课程，当然从国内大多院校情况来看：

《数据结构》介绍了如何将对象用某种数据形式表示并有组织地存放在计算机中, 是计算机专
业的一门重要课程.该课程也涉及算法, 但仅限于实现相关数据形式的
查找、排序、遍历、增删等操作

《算法设计》是脱离具体数据结构来研究求解问题的方法课程，介绍的方法是一些具有抽象性的普遍应用的方法。

算 法 (Algorithm) 是任何一个良好 定 义 (welldefined)的计算过程, 它接收某个值或值的集合作为输入, 产生某个值或值的集合作为输出。

因此, 一个算法是一个计算步骤的序列, 这些步骤
将输入转化为输出，如下图所示：

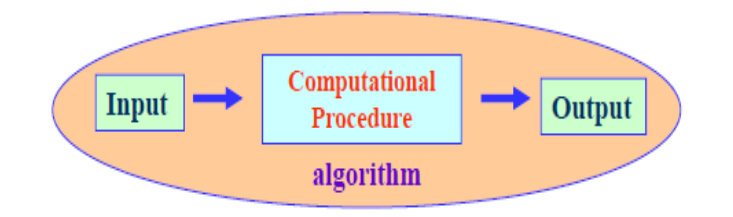
通俗地讲, 算法是指解决问题的一种方法或一个过程.

严格地讲，算法是由若干条指令组成的有穷序列，且满足如下性质：

• 输入：有零个或多个外部提供的量作为算法的输入.

• 输出：算法产生至少一个量作为输出.

• 确定性：组成算法的每条指令是清晰, 无歧义的.

• 有限性：算法中每条指令的执行次数是有限的, 执行
  每条指令的时间也是有限的. (可行性)

程序可以不满足算法的有限性。

说通俗一些, 算法是解决一个问题的思路，
程序则是解决这些问题所具体好写的代码。 

算法没有语言界限，它只是一个思路。为实现相同的一个算法，用不同语言编写的程序
会不一样。 

算法是写程序的思想，程序是算法的体现。

【算法描述方法】

一个算法的描述方法可以通过四个工具来实现：

1、自然语言

2、流程图

3、程序设计语言

4、伪代码

至于其中实现不在此详细叙述。

【问题与问题求解】

问题(Problem)：规定了输入与输出之间的关系，
可以用通用语言来描述。 

问题求解(problem solving)是寻找一种方法来实现
目标。 

问题求解过程(problem solving process)是人们通
过使用问题领域知识来理解和定义问题，并凭借自身的经验和知识去选择和使用适当的问题求解
策略、技术和工具，将一个问题描述转换成问题
解的过程。 

计算机求解问题的关键之一是寻找一种问题求解策略(problem solving strategy)，得到求解问题的算法，从而得到问题的解。

【常见应用问题类型】

1. 查找问题

   查找(搜索)：在给定的数据集合中寻找满足条件的数据对象。

   例：

   在图书管理中，若要了解全部读者的借阅信息，就需要对每一位读者的借阅记录依次输出，这是数据对象的遍历问题。

   如果我们要查找借书超期的读者，则是按照规定的最大借书期限这一特征值去查找满足该条件的记录。

2. 排序问题

   排序：把一组无序的数据按照一定的规则排列起来。排序结果有升序和降序两种。

   例：为便于查询学生的考试成绩，对于成绩单,通常按照学号排序；而在招生录取中，也可以按
   照成绩的高低排序。

   对于同一个问题，排序的算法是多种的，如插入排序、选择排序、交换排序等。

3. 图问题

   图问题主要是研究数据结构是图结构或树结构的算法问题。简单的定义，可以认为图是由一些顶点和顶点之间的边所构成的集合。

   图结构可以用来对各种各样的实际应用问题建模，包括交通和通讯网络、工程项目时间表和各种竞赛。

   图应用算法主要包括图的遍历算法、最短路径算法、最小生成树算法、拓扑排序算法和网络流算法等。

4. 组合问题

   有一些问题要求寻找一个组合对象，比如一个排列、一个组合或者一个子集，这些对象能够满足特定的条件并
   具有我们想要的特性(如价值最大化或者成本最小化)。从
   更抽象的角度来看这类问题是组合问题。

   例：旅行售货商问题、图着色问题

   组合问题所涉及的应用领域更加广阔，例如拓扑学、图论、博弈论、线性规划等。组合问题的特点是随着问题规模的增加，已达到计算机的处理能力的极限。所以,称组合问题是计算机中的难解问题。

5. 几何问题

   几何算法处理类似于点、线、多面体这样的几何对象。

   例：经典的计算几何问题

   最近点对问题求的是给定平面上的n个点中，寻找距离最近的两个点。

   凸包问题要求找一个能把给定集合中所有点包含都在 里面最小凸多边形。

   当前，几何问题算法在计算机图形学、机器人技 术和断层X摄像技术等方面都有广泛的应用。

6. 数值问题
   

        数值问题是另一大类问题，它要解决的问题包括：求解方程或者方程组和求数值积分等。

        这些问题常常只能给出一个近似的结果，而不是精确的解析答案。

【问题求解过程】

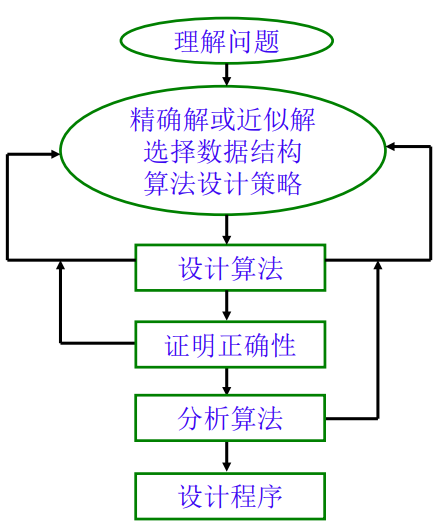
注：

理解问题: 是否属于已知问题？确定算法输入范围； 

了解计算设备的性能: 清楚速度和计算资源的限制； 

在精确解法和近似解法之间做选择: 有时近似算法是唯一选择；

确定适当的数据结构 

算法设计技术: 

算法描述: 自然语言、流程图、伪代码； 

算法正确性证明: 证明对于所有合法输入均能产生正确结果；

算法分析: 分析执行效率(时间和空间)、简单性、一般性；

设计程序: 利用编程语言以计算机程序实现算法.

【算法设计方法-经典算法】

• 分治法

• 动态规划法

• 贪心法

• 回溯法

• 分支限界法

• 线性规划与网络流算法

…