【算法设计与分析】概述（二）—<复杂性>

【一条公式引入复杂性】

\( C = F(N, I, A)\)

【概述】

目前公认的算法复杂性的理解即算法所需要的计算机资源。我们引入几个复杂性概念：

• 时间复杂性\( T(n)\) ：在计算机中执行算法需要的时间资源量

• 空间复杂性\( S(n)\) ：在计算机中执行算法需要的空间资源量

• 问题规模\( n\)： 算法的待解空间即：输入的大小

如果分别用N、I和A表示算法要解问题的规模、算法的输入和算法本身, 而且用C表示复杂性,那么, 应该有:

\( C = F(N, I, A)\)

而一般把时间复杂性和空间复杂性分开，并分别用\( T\) 和\( S\)来表示，则有：

\( T = T(N, I)\)

\( S = S(N, I)\)

(通常将\( A \)隐含在复杂性函数中)

【计算推导】

在算法中，我们假设元运算有\( k \)种：

\( O_1, O_2, \dots, O_k\)

执行元运算时间分别为：

\(t_1, t_2, \dots, t_k\)

假设用到元运算的次数分别为：

\( e_1, e_2, \dots, e_k\)

其中：

\( e_i = e_i(N, I)\)

那么则有：

\(\begin{align} T(N, I) = \sum_{i=1}^{k} t_i e_i(N, I)\end{align}\) 

由于不可能对规模为N的每一种合法输入I都去统计运算次数，只能在某些代表性的合法输入中进行统计。于是我们将\( T(N, I) 和 S(N, I)\)进一步简化为\( T(N) 和 S(N)\)

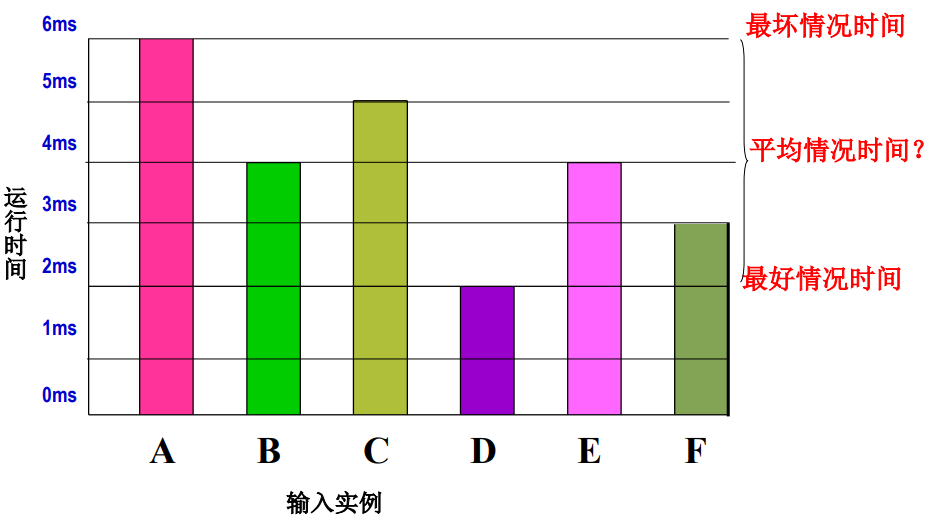
【进一步引入复杂性】

上文中我们已经知道\( T(n) \)是如何一步步简化的，下面我们从时间复杂度来进一步引入复杂性分析有关内容。

三种情况下的时间复杂性：

• 最坏情况：指问题规模为\( N \)时任何输入中的最长运行时间。其数学表达如下：

\(\begin{align} T_{max} (N) = \max_{I \in D_N} T(N, I) = \max_{I \in D_N} \sum_{i = 1}^k t_i e_i(N, I^*) = T(N, I^*)\end{align}\)

• 最好情况：指问题规模为\(\begin{align} N\end{align}\)时任何输入中的最短运行时间，其数学表达如下：

\(\begin{align} T_{min} (N) = \min_{I \in D_N} T(N, I) = \min_{I \in D_n} \sum_{i = 1}^k t_i e_i(N, I) = \sum_{i = 1} ^ k t_i e_i (N, \widetilde{I}) = T(N, \widetilde{I}) \end{align}\)

• 平均情况：指问题规模为\(\begin{align} N\end{align}\)时任何输入中的平均运行时间，其数学表达如下：

\(\begin{align} T_{avg}(N) = \sum_{I \in D_N}P(I) T(N, I) = \sum_{I \in D_N} P(I)\sum_{i = 1} ^{k} t_i e_i(N, I)\end{align}\)

其中：

• \(\begin{align} D_N\end{align}\)是规模为\(\begin{align} N\end{align}\)的合法输入的集合

• \(\begin{align} I^*\end{align}\)是\(\begin{align} D_N\end{align}\)中使得\(\begin{align} T\end{align}\)达到\(\begin{align} T_{max}(N)\end{align}\)的合法输入

• \(\begin{align} \widetilde{I}\end{align}\)是\(\begin{align} D_N\end{align}\)中使得\(\begin{align} T\end{align}\)达到\(\begin{align} T_min{N}\end{align}\)的合法输入

• \(\begin{align} P(I)\end{align}\)是算法的应用中输入\(\begin{align} I\end{align}\)出现的频率

其示意图如下图所示:

补充：

关于最坏情况的时间分析：

• 它是算法对于任何输入的运行时间的上界; 

• 对于某些算法, 最坏情况常常发生, 如在DB中搜索一个并不存在的记录; 

• 平均时间往往和最坏时间相当(常数因子相同). 

关于平均运行时间：

• 常常假定一个给定问题规模的所有输入是等概率的. 实际上这种可能并不一定成立,但可以用随机化算法强迫它成立. 

• 有时平均时间和最坏时间不是同数量级, 算法选择依据是: 最好、最坏的概率较小时,尽量选择平均时间较小的算法.

【复杂性的进阶分析-渐进性态】

定义如下：

设\(T(N)\)为算法A的时间复杂性函数，则它是\( n\)的单调增函数

如果存在一个函数\(\widetilde{T}(n) \)

使得当\(n \rightarrow \infty \)时有: 

\( \frac{T(n) – \widetilde{T}(n)}{T(n)} \rightarrow 0 \)

那么我们称\(\widetilde{T}(n) \)是\( T(n)\)当\( n \rightarrow \infty\)时的渐进性态或渐进时间复杂性

在数学上 

\( T(n)\)与\( \widetilde{T}(n)\)有相同的最高阶项, 可取\( \widetilde{T}(n)\)为略去\( T(n)\)的低阶项后剩余的主项. 

当n充分大时我们用\( \widetilde{T}(n)\)代替\( T(n)\)作为算法复杂性的度量, 从而简化分析. 

例如

\( T(n) = 3n^2 + 4n\log{n} + 7\), 则\( \widetilde{T}(n)\)可以是\( 3n^2\). 

若进一步假定算法中所有不同元运算的单位执行时间相同, 则可不考虑\( \widetilde{T}(n)\)所包含的系数或常数因子, 只表征出以影响算法运行时间的主要因素\(n^2 \).

【渐进分析记号定义】

• 渐进上界:\( O\)

\( O(g(n)) = \{ f(n) | 存在正常数c和n_0 使得对所有n \geq n_0 有: 0 \leq f(n) \leq cg(n)\}\)

• 渐进下界:\( \Omega\)

\( \Omega (g(n))= \{f(n)|存在正常数c和n_0使得对所有n \geq n_0 有: 0 \leq cg(n) \leq f(n) \} \)

• 非紧上界:\( o\)

\( o(g(n)) = \{ f(n) | 对于任何正常数c > 0, 存在正常数n_0 >0 使得对所有 n \geq n_0有： 0 \leq f(n) < cg(n) \}\)

等价于：

\(\begin{align}\lim_{n \rightarrow 0}\frac{f(n)}{g(n)} = 0 \end{align}\)

• 非紧下界:\(\omega \)

等价于：

\(\begin{align} \lim_{n \rightarrow 0} \frac{f(n)}{g(n)} = \infty\end{align}\)

结合上述得出：

\(f(n) \in \omega(g(n)) \Leftrightarrow g(n) \in o(f(n))\)

• 紧渐进界:\( \Theta\)

\( \Theta (g(n)) = \{ f(n) | 存在正常数c_1, c_2和n_0使得对所有n \geq n_0有c_1g(n) \leq f(n) \leq c_2g(n) \}\)

定理：

\( \Theta(g(n)) = O(g(n)) \cap \Omega (g(n))\)

【渐进分析记号的意义】

• \( f(n) = \Theta(g(n))\)的确切意义是: \( f(n) \in \Theta(g(n))\)

• 一般情况下，等式和不等式中的渐进记号\( \Theta(g(n))\)表示\( \Theta(g(n))\)中的某个函数。

        如：

        \( 2n^2 + 3n + 1 = 2n*2 + \Theta(n)\)表示\( 2n^2 + 3n + 1 = 2n^2 + f(n)\), 其中\( f(n)\)是\( \Theta(n)\)中某个函数.

• 等式和不等式中渐进记号\( O, o , \Omega , \omega\)的意义类似

【关于\( O\)的解释】

大\( O \)表示法（算法运行的上界）：

        若存在正常数\( c\)和自然数\( n_0\)使得当\( n \geq n_0\)时，有\( 0 \leq f(n) \leq cg(n)\)，则称函数\( f(n)\)在\(n \)充分大时有上界，且\( g(n)\)是它的一个上界，记为\( f(n) = O(g(n))\), 也称\( f(n)\)的阶不高于\( g(n)\)的阶。

图像表达如下：

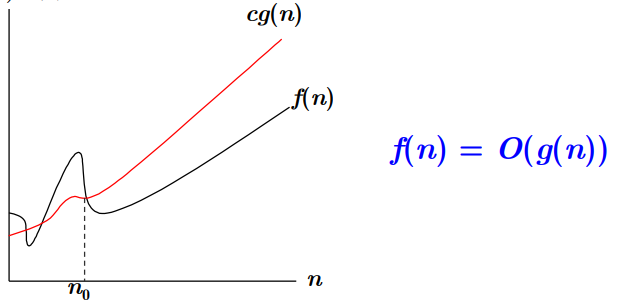
注意：

当说一个算法具有\(O(g(n))\)的计算时间时, 指的是如果此算法用\(n\)值不变的同一类数据在某台机器上运行时, 所用的时间总是小于\(g(n)\)的一个常数倍. 

所以, 从计算时间来说, \(f(n)\)的数量级就是\(g(n)\). 当然, 在确定\(f(n)\)的数量级时总是希望求出最小的\(g(n)\), 使得\(f(n)=O(g(n))\).

例如：

• \( 3n = O(n)\)
• \( n + 1024 = O(n)\)

• \( 2n^2 + 11n – 10 = O(n)\)

• \( n^2 = O(n^3)\)

• \( n^3 \neq O(n^2)\)

运算法则：

• \( O(f(n)) + O(g(n)) = O(\max{f(n), g(n)})\)
• \( O(f(n)) + O(g(n)) = O(f(n) +g(n))\)
• \(O(f(n)) \times O(g(n)) = O(f(n) \times g(n)) \)
• \(O(cf(n))  = O(f(n))\)
• \(g(n) = O(f(n)) \Rightarrow O(f(n)) + O(g(n)) = O(f(n)) \)
• \( f(n) = O(f(n))\)

【常见的复杂性函数】

【不同规模数据复杂度对比图】

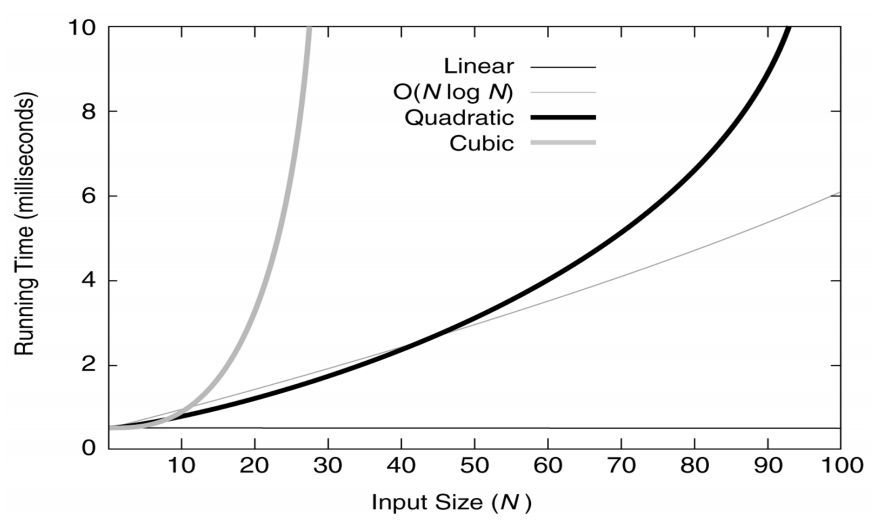
小规模数据复杂度示意图

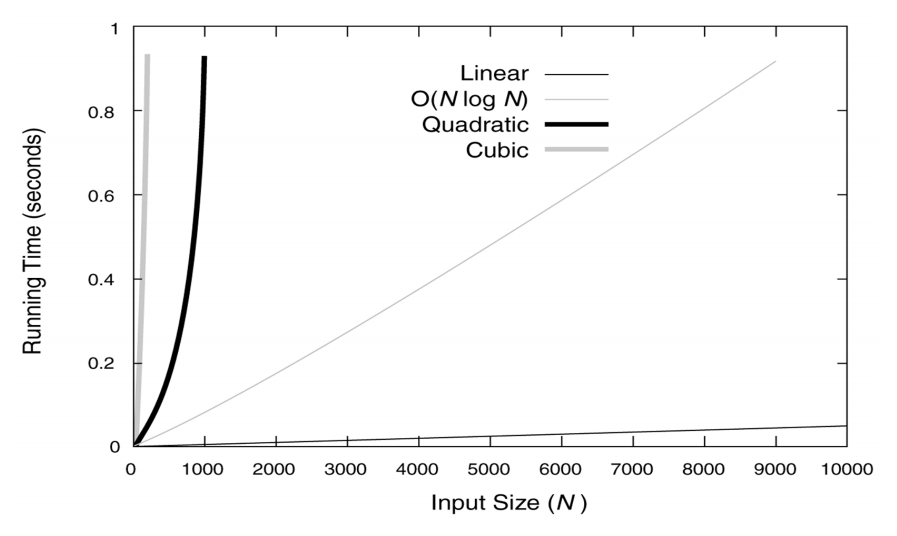
中等规模数据复杂度示意图

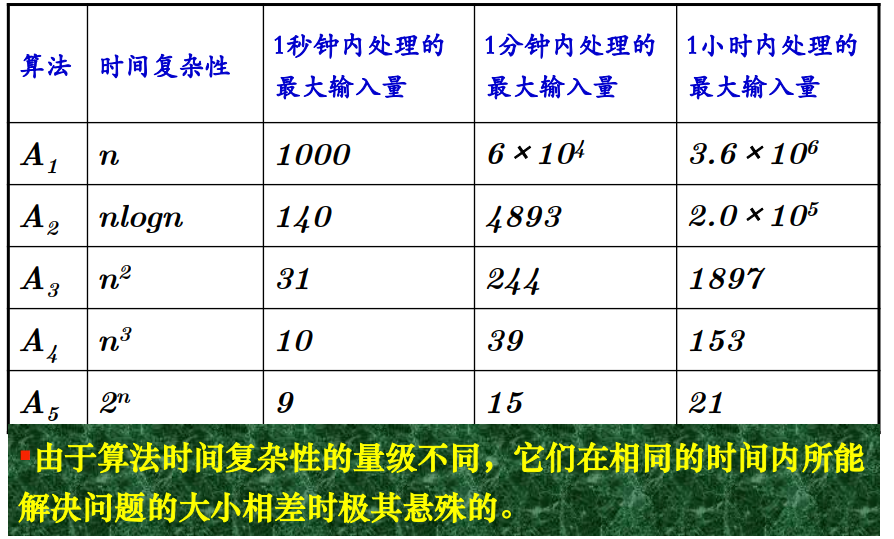
【不同算法输入量上界】

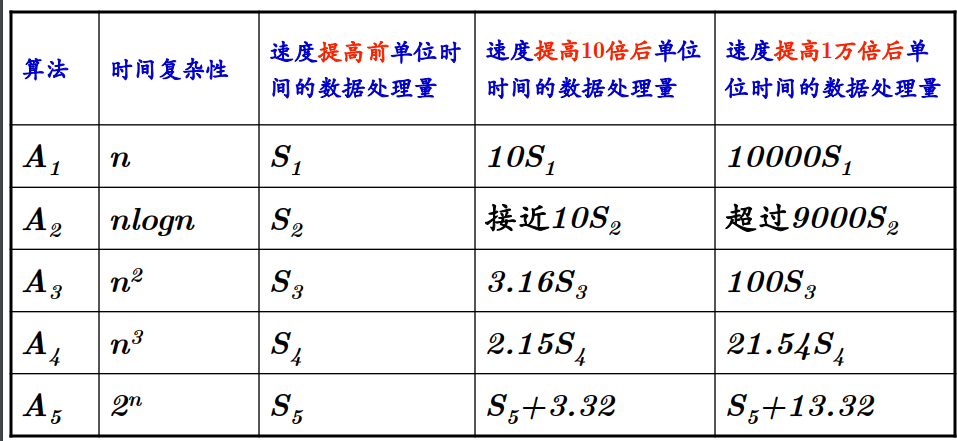
【提高计算机速度对算法的优化效果】

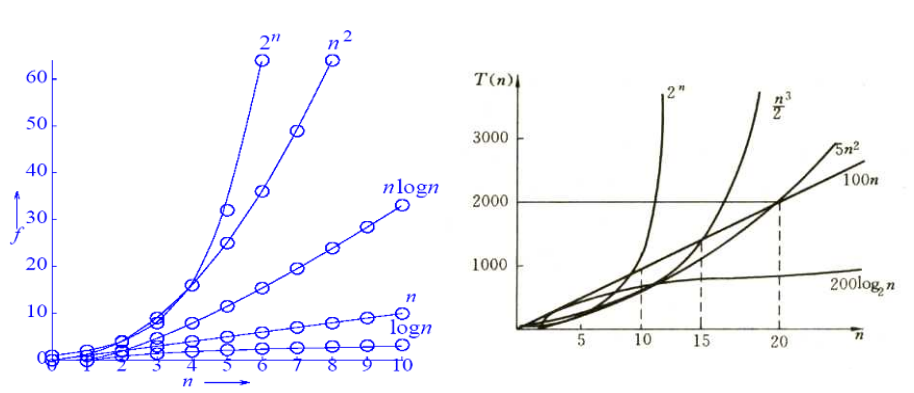
【常见的算法时间复杂性函数对比】

【一些结论】

结论: 算法的渐近复杂性的阶对于算法的效率有着决定性的意义.

多项式复杂度的算法：

如果一算法的最坏情形时间复杂度\(T(n)=O(n^k)\),则称该算法为多项式复杂度的算法.

计算机科学家普遍认为, 一个多项式复杂度的算法是有效算法, 即: 对于一个有效算法, 哪怕输入量很大, 计算机仍然可以处理得了.

【参考资料】

• 2019年广西师范大学计算机与信息工程学院算法设计与分析课件[OL].李志欣教授.2019.01.01