【基本思想】
将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
【适用条件】
该问题的规模缩小到一定的程度就可以容易地解决;
该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
利用该问题分解出的子问题的解可以合并为该问题的解;
该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题;
【基本步骤】
分治法的三个步骤:
(1) 分解(Divide):
将原问题分成成一系列子问题;
(2) 求解(Conquer):
递归地解各个子问题。若子问题足够小,则直接求解;
(3) 合并(Combine):
将子问题的结果合并成原问题的解
【设计模式】
divide-and-conquer(P){
if(|P| <= n0){
adhoc(P); //解决小规模问题
}
divide P into smaller subinstances P1,P2, ...Pk //分解子问题
for(i = 1; j <= k; i++){
yi = divide-and-conquer(Pi); //递归求解子问题
}
return merge(y1,...,yk); //合并子问题
}
【启发式规则】
平衡子问题:
在用分治法设计算法时,最好使子问题的规模大致相同。也就是将一个问题划分成大小相等的k个子问题(通常k=2),这种使子问题规模大致相等的做法是出自一种平衡(Balancing)子问题的思想,它几乎总是比子问题规模不等的做法要好。
独立子问题:
各子问题之间相互独立,这涉及到分治法的效率,如果各子问题不是独立的,则分治法需要重复地解公共的子问题。
【典型情况】
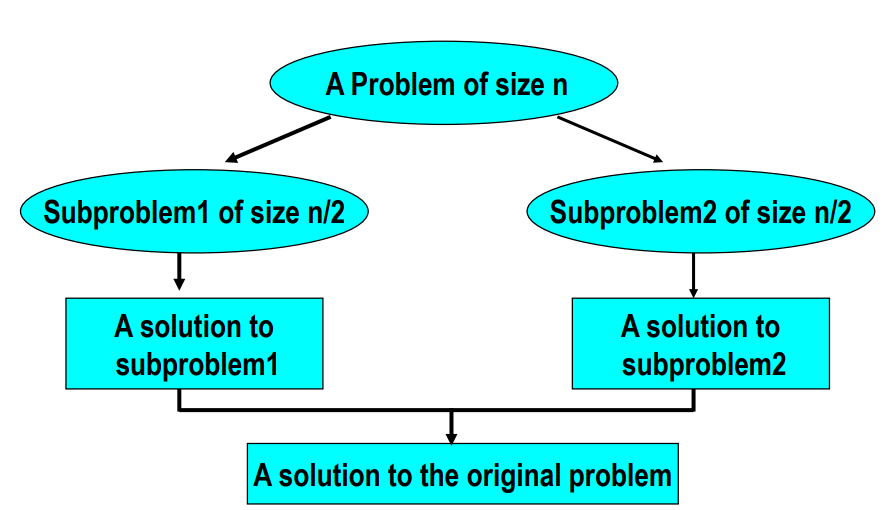
【复杂度分析】
一个分治法将规模为n的问题分成k个规模为n/m的子问题去解. 设分解阀值n0=1, 且解规模为1的问题耗费1个单位时间, 再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间. 用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间, 则有:
\(T(n) = \begin{cases} O(1) && n= 1\\ kT(n/m) + f(n) &&n > 1\end{cases} \)
注意:递归方程及其解只给出n等于m的方幂时T(n)的值,但是如果认为T(n)足够平滑,那么由n等于m的方幂时T(n)的值可以估计T(n)的增长速度。通常假定T(n)是单调上升的,从而当mi≤n<mi+1时,T(mi)≤T(n)<T(mi+1)。
【应用举例】
Strassen矩阵乘法(分治、剪枝)[附Python源码]
【参考文献】
-
2019年广西师范大学计算机与信息工程学院算法设计与分析课件[OL].李志欣教授.2019.01.01
[…] 20190304 20190304 […]