【数学】向量微积分基础-雅克比矩阵（Jacobian matrix）

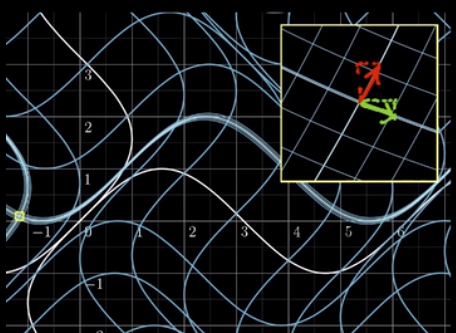
【背景】

        看了论文发现看不懂这些专业基础，那就恶补一下向量微积分吧。

【引言】

        其实很多在多元微积分中所学到的概念都是在原来学习到的基础和思想上演变而来的，比如我们学过线性代数，那么我们就可以把它的变换思想转换到非线性问题。

【问题引入】

        假定给出一个函数，这个函数输入二维变量，输出也是二维变量。定义如下：

$f(\left[\begin{array}{c}x\\ y\end{array}\right])=\left[\begin{array}{c}x+\cos (y)\\ y+\cos (x)\end{array}\right]$

【线性变换可视化】

        利用matlab等工具，我们将$\left[\begin{array}{c}x\\ y\end{array}\right]$(上图)移动到$\left[\begin{array}{c}x+\sin (y)\\ y+\sin (x)\end{array}\right]$（下图）

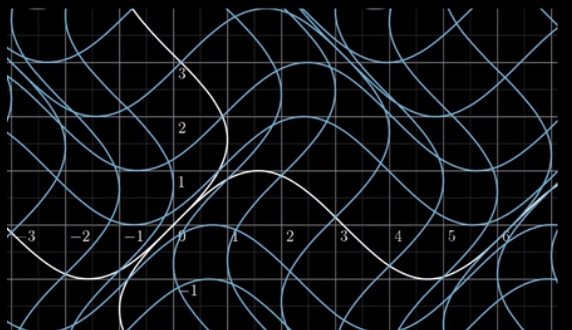
        两幅图对比中，我们可以知道，在经过简单的非线性变化之后，图像变得非常扭曲。它的所有输出线不是平行且分布均匀的网格线。从某种意义上讲，相对于线性函数，非线性函数能引入的信息将更多。

【局部分析】

        为了弄清楚这个非线性变换到底是如何运转的，我们针对某个特殊点进行分析。

我们取$\left[\begin{array}{c}\pi /2\\ 0\end{array}\right]$,将它变成$\left[\begin{array}{c}\pi /2+\sin 0\\ 0+\sin \frac{\pi }{2}\end{array}\right]$.即$\left[\begin{array}{c}\pi /2\\ 1\end{array}\right]$.

我们专注这个点，通过两图对比分析。

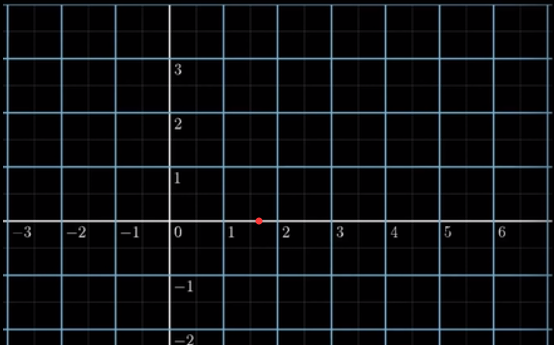
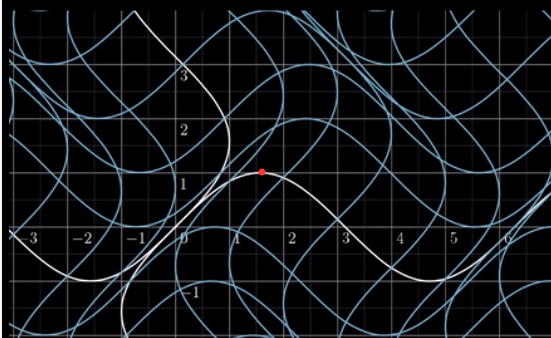
        在空间上，只是垂直平移了一个单位。

        当然，整体的变换时很复杂的，因为每个点都在变。在对比了线性变换，并用矩阵编码的思想后，这种非线性变换就让人感到非常棘手。我们必须编码更多的信息才能得到这个变换，而不是只用简单的四个数字的二维矩阵就能掌握。但是这些函数变换也有一些比较简单的性质。一个在我们整个微积分的学习都能见到的性质。那就是局部线性（Locally Linear）.

【局部线性】

        我们在某一点的附近再加入更多的网格线，并将其放大显示于左边系右侧，如图所示：

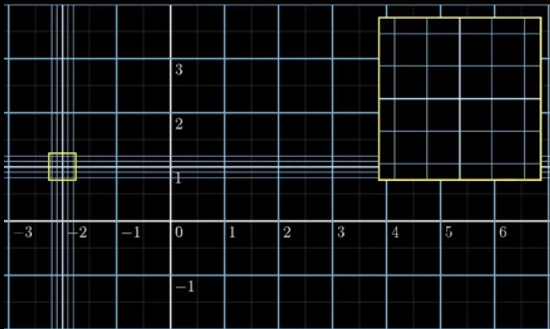
我们将其进行函数变换得到下图：

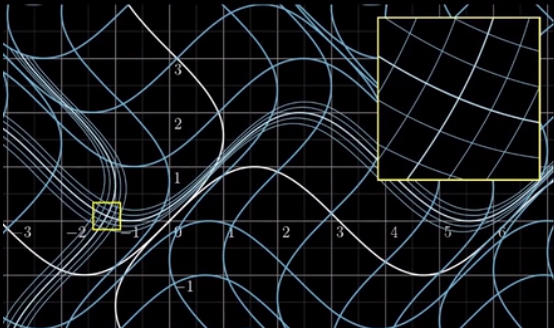
        我们在这个放大的视角中发现这个变换仍不是线性的，这些线仍有点弯。但是它们看起来比刚刚看到的更像一个线性函数了，这些线更像网格线。

再进一步地放大，并添加更密集的网格线。结果如下图。

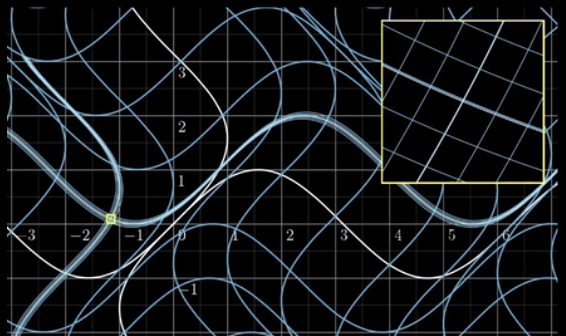
我们可以看到它更像一个线性函数变换了。

        于是我们假设，我们将视角越放大，将网格线越细分，这个变换就越近似于线性函数变换。我们称这样的特性为：局部线性

        如果我们观察一个特定的点周围，称之为$\left[\begin{array}{c}{x}_0\\ y_0\end{array}\right]$,这个点附近的变换应该对应着某种线性变换。应该会有某个$2\times 2$矩阵表示像这个如此复杂函数再某个点局部的线性变换。总的来说，这种放大的思想就是我们说的局部线性。

【Jacobian Matrix】

        回到引入的问题，$f$表示一种变换，这种变换把空间上的每一个点$(x,y)$带到$(x+\sin (y),y+\sin (x))$上。在上一章节中，我们将点（-2， 1）（在此进行实例化），进行放大观察，并添加更细粒度的网格线，我们能观察到这个变换再这个点附近的细节。即使这个函数整体的变换时很复杂的，但是这个点的附近的变换确是很线性的。上一节提及到的$2\times 2$矩阵可以表示这个局部线性函数。

回到最初的模型，我们将点考虑向右走一小步(偏向(x)$\partial x$微小的沿着x方向的一小步。)

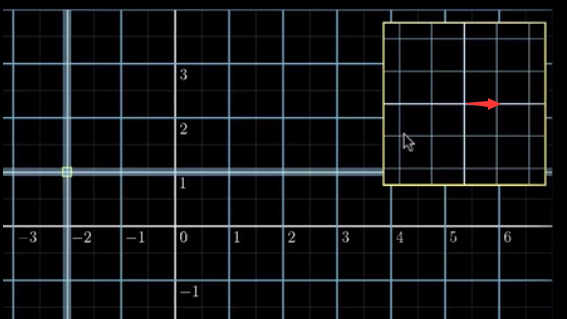
在线性变换后：

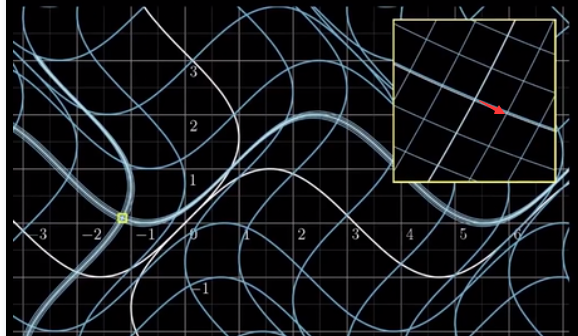
它也会变成再输出空间中的一小步，但它不再是单纯沿着x方向了，它除了有了一点向右的分量，还有一点向下的分量。为了更好地表示这两个分量，我们将原问题重新定义为：

$\left[\begin{array}{c}{f}_1(x,y)\\ f_2(x,y)\end{array}\right]=\left[\begin{array}{c}x+\sin (y)\\ y+\sin (x)\end{array}\right]$

第一个分量表示为下图：

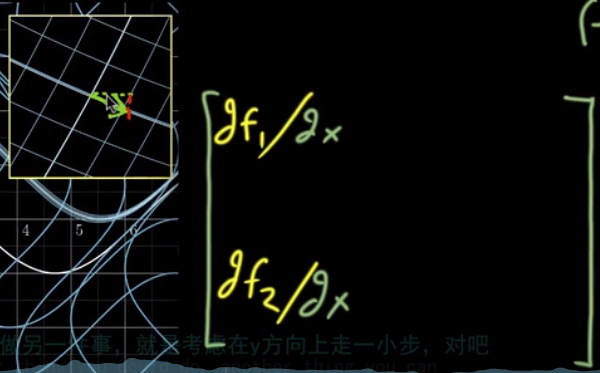
再考虑在y方向上走一步。

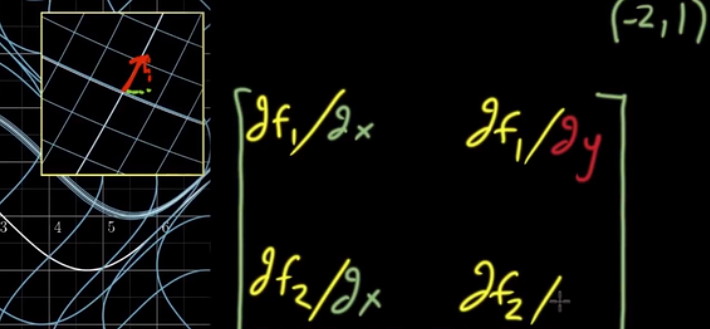
得到的充满偏导的矩阵称为：Jacobian Matrix(雅克比矩阵)。我们可以理解它为携带了所有的偏微分信息。它同时考虑了所有可能的输入和输出分量，并且给了表示所有这些偏导的网格线。当然，这不仅仅是一种记录所有可能的偏导的方式，这么把他们（偏导）组合在一起，成为矩阵，是有原因的，这归功于局部线性的思想。雅可比矩阵从根本上应该代表了，当你放大一个特定点的附近时变换的样子。

【直观体现】

先将上一章节求出来的导数代入问题。得到雅克比矩阵结果：

$\left[\begin{array}{cc}1& \cos (y)\\ \cos (x)& 1\end{array}\right]$

将(-2, 1)代入上式得：

$\left[\begin{array}{cc}1& 0.54\\ -0.42& 1\end{array}\right]$

观察图像：

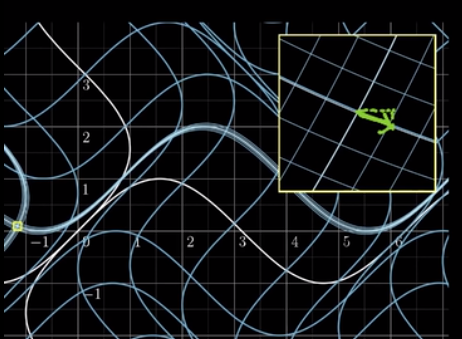
第一个分量坐标是近似于（1, -0.42）的

而第二个分量同样近似于(0.54,1)的

【参考文献】

• （干货）《雅可比矩阵是什么东西》3Blue1Brown，搬自可汗学院。 【自制中文字幕】