【数学】向量微积分基础-雅克比行列式(Jacobian Determinant)

【引言】

        正如其名，雅克比行列式或多或少的可以说是雅可比矩阵(Jacobian Matrix)的行列式（但是有一些条件），我们先回顾一下线性代数中的行列式这个概念本身代表了什么，在普通的线性代数中，我们假设某个矩阵的行列式形如：

$\det (\left[\begin{array}{cc}3& 0\\ 1& 2\end{array}\right])$

        我们用对角线法则计算出它的值是$3\times 2–0\times 1=6$,但我们知道，行列式不仅仅是代表着一个简单的计算，从几何解释上来说，如果我们认为矩阵$\left[\begin{array}{cc}3& 0\\ 1& 2\end{array}\right]$作为一个线性变换，那么这个变换将第一个基向量带到坐标$(3,0)$，并把第二个基向量带刀坐标$(1,2)$。将矩阵从行列式角度上思考，我们一般认为行列式从某种角度上衡量了这个变换对空间的伸缩挤压的大小。具体看下图：

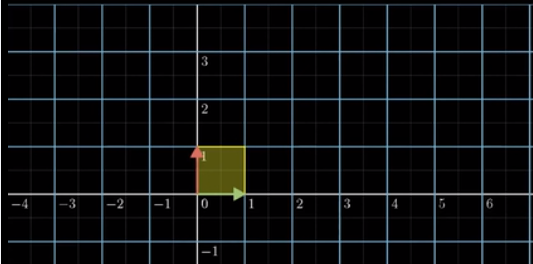
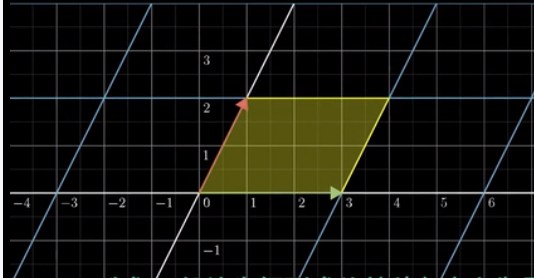
        我们注意到，这个黄色区域变换前是一个方块，一个边长为一的正方形，面积为1，变换之后比较一下它们，变换之后，这个面积被拉伸了多少，答案显而易见，就是行列式的计算结果。

【Jacobian determinant】

        从行列式的角度上来看，雅可比矩阵有什么特殊的性质？回到上一篇文章讲述的问题背景。对于一个扭曲的非线性变换，我们对某个点进行放大观察（局部线性）。从区域回顾它的变换特性：

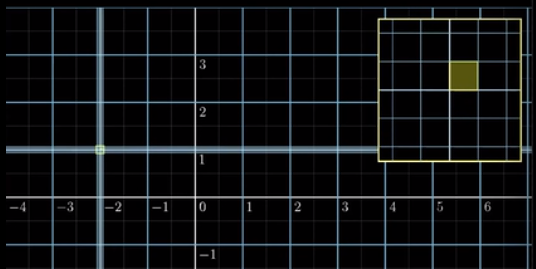
上图中的黄色区域（变换前）是线性的，我们对其变换后得到下图：

        整幅图我们可以看到，线条是呈弯弯曲曲状的，但是在放大视角上来看，这块区域却像一个线性函数。不妨假设，如果我们能知道，描述这个放大的细微区域中变换的矩阵，那么利用这个矩阵的行列式就可以告知我们这个微小面积拉伸的比例。而这个变换矩阵就是我们上一篇文章中介绍的雅克比矩阵（Jacobian Matrix）,回到上一篇文章中的问题空间。我们直接引用该变换的雅克比矩阵：

$\left[\begin{array}{cc}\frac{\partial f_1}{\partial x}& \frac{\partial f_1}{\partial y}\\ \frac{\partial f_2}{\partial x}& \frac{\partial f_2}{\partial y}\end{array}\right]$

代入问题空间有：

$\left[\begin{array}{cc}1& \cos (y)\\ \cos (x)& 1\end{array}\right]$

将点$(-2,1)$代入有：

$\left[\begin{array}{cc}1& 0.54\\ -0.42& 1\end{array}\right]$

计算其行列式得结果约为： 1-(-0.227)=1.227

        这意味着$(-2,1)$这个点附近的空间伸缩了1.227倍，我们对比上下图观察到黄色区域似乎伸展了一点，但也不是很多。也大约是1.227倍。

作为对比，我们选取另一个点$(0,1)$

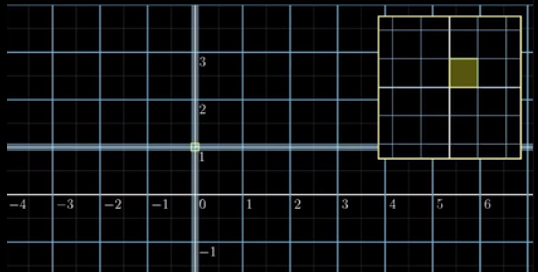
        再对Jacobian determinant计算，得出结果$1–\cos (0)\cos (1)=0.46$

观察下图。

        根据我们的计算，得出结论，黄色区域大约缩小了到0.46倍，这就是这个行列式的意义。

【结论】

        这是行列式一个有意思的性质：就是当我们关注一个点足够小的局部区域，要得到一个直观的感受。再某个点局部微分区域是伸展了还是收缩了，并且伸展或收缩了确切的多少倍这就是雅克比行列式的意义，而这个概念的建立就是解决局部空间伸缩问题的。

【参考文献】

• 《雅可比矩阵下：所谓的雅可比行列式》3Blue1Brown Grant Sanderson，搬自可汗学院。 【自制中文字幕】