【论文笔记】Bidirectional Learning for Domain Adaptation of Semantic Segmentation

【背景】

        最近研究域自适应语义分割，看到两篇比较好玩的文章。遂记录下来，供今后找点灵感。

【论文描述/动机】

        用于语义图像分割的域自适应是非常必要的，因为用像素级标签手动标记大型数据集既昂贵又耗时。现有的域适应技术要么在有限的数据集上工作，要么与监督学习相比产生不那么好的性能。本文提出了一种新的双向学习框架，用于分割的域适应。使用双向学习，图像翻译模型和分割适应模型可以交替学习并相互促进。此外，提出了一种自监督学习算法来学习更好的分割自适应模型，从而改进图像翻译模型。

【论文介绍】

文章先对经典的域自适应方法进行了分析：

1、经典域自适应的做法是利用对抗学习最小化源分布和目标分布之间的一些距离度量（两个常用的度量是一阶和二阶矩）。用这两种常用的距离度量在一些分类任务上取得了很大的性能提升，但是在语义分割任务上表现并不突出。

2、还有一些做法是将两种度量进行了分离，将他们视为两个任务进行。具体做法如下：

2.1、先使用图像到图像的翻译模型将图像从源域翻译到目标域（pix2pix/cycleGAN）

2.2、然后，在分割模型的特征上添加鉴别器，以进一步减小域间隙

        当前一步减少了域间隙时，后一步容易学习，可以进一步减少域偏移，但我们知道分割模型非常依赖于图像到图像的翻译质量。一旦图像到图像的翻译失败或者效果不那么明显，在接下来的阶段就无法弥补了。

        为解决上述提及的各方面存在的问题，本文用一种Bidirectional Learning trick，巧妙地缓解了这些问题。并引入一种自学习策略（SSL），应用于双向学习的感知损失，进一步提升了网络表现。

【双向学习/Bidirectional Learning】

        上文我们也介绍到，现阶段分离两种度量视为两类任务并顺序执行。一、用图像翻译成图像，初步缩减源域与目标域的域隔阂。二、将翻译后的源域图像以及目标域图像输入一个经典的域自适应语义分割网络。计算其对抗损失，分割损失并最小化它们。从宏观的角度上我们可以抽象成文章中提及的顺序学习。

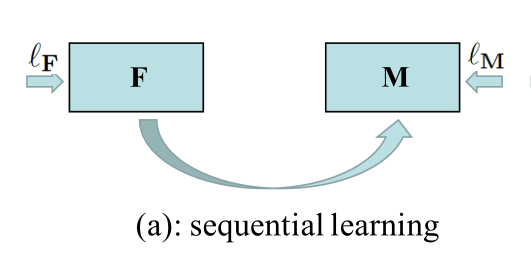
分析中也提及到，这种学习模式中M（传统的域自适应模型）极度依赖来自F（图像翻译模型）的结果，如果F产生的结果表现并不好，那么M所产生的效果也不好。

于是作者试想，能否添加一条数据反馈M->F达到双向制约的目的？最终的双向学习模型如下：

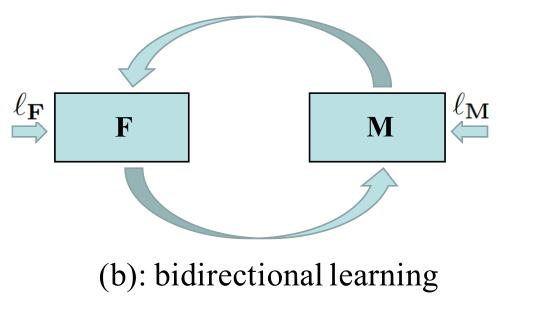
在F->M方向上作者加入了一些tricks。这个过程中作者提出了一种自监督学习方法，具体做法就是在网络训练过程中，对于目标域数据（真实数据）输送至网络后会产生结果，作者设置了一个阈值，将高置信度的结果近似为Ground-Truth结果，而排除低近置信度结果，将这些高置信度结果用以更新分割网络模型。这样做，类似于半监督模型，使用伪标签改善了M的表现，同时在接下来的M->F反馈中也能起到更好地感知作用。

再M->F方向上，模型通过分段式迭代改进，引入了一种新的感知损失，在像素级上对齐分割图像与翻译结果之间的语义一致性，从而搭建出M->F之间的桥梁，利用翻译模型中的约束，可以进一步减小翻译图像和真实数据集(目标)之间的视觉外观(例如，照明、对象纹理)的差距。

【模型细节】

我们从大局上了解了整个框架的数据流向，现在从细节上对模型进行叙述。

        在F->M方向上，与一些经典的顺序网络一样。首先用源域图像$\mathcal{S}$和目标域图像$\mathcal{T}$训练图像翻译网络F。训练结束过后从F中我们得到${\mathcal{S}}^{{}^{\prime }}$，这里需要注意的是，源域数据在经过F后，只是将图像进一步对其目标域图像，并不将它的标签进行改动。即$Y_{\mathcal{S}}$是不变的。得到${\mathcal{S}}^{{}^{\prime }}$后，将${\mathcal{S}}^{{}^{\prime }}$和$\mathcal{T}$送入分割网络。并用$Y_{\mathcal{S}}$计算源域的分割损失。用鉴别器进一步对其目标域与源域的边缘概率。其中M部分计算损失如下：

$\begin{array}{rl}{\mathcal{L}}_M=& {\lambda }_{\mathrm{adv}}{\ell }_{\mathrm{adv}}(M({\mathcal{S}}^{{}^{\prime }}),M(\mathcal{T}))\\ & +{\ell }_{\mathrm{seg}}(M({\mathcal{S}}^{{}^{\prime }}),Y_{\mathcal{S}})\end{array}$

对于F的模型，我们从M->F方向上重新设计其损失（与图像翻译网络适配）。其损失计算如下：

$\begin{array}{rl}{\mathcal{L}}_F& ={\lambda }_{\mathrm{GAN}}[{\ell }_{\mathrm{GAN}}({\mathcal{S}}^{{}^{\prime }},\mathcal{T})+{\ell }_{\mathrm{GAN}}(\mathcal{S},{\mathcal{T}}^{{}^{\prime }})]\\ & +{\lambda }_{\mathrm{recon}}[{\ell }_{\mathrm{recon}}(\mathcal{S},{\mathrm{F}}^{-1}({\mathcal{S}}^{{}^{\prime }}))+{\ell }_{\mathrm{recon}}(\mathcal{T},\mathrm{F}({\mathcal{T}}^{{}^{\prime }}))]\\ & +{\ell }_{\mathrm{per}}(\mathrm{M}(\mathcal{S}),\mathrm{M}({\mathcal{S}}^{{}^{\prime }}))+{\ell }_{\mathrm{per}}(\mathrm{M}(\mathcal{T}),\mathrm{M}({\mathcal{T}}^{{}^{\prime }}))\end{array}$

为了确保图像翻译图像的一致性，这三个损失是同时计算的。GAN网络损失强制对齐${\mathcal{S}}^{{}^{\prime }}$和$\mathcal{T}$的边缘概率。而${\mathcal{T}}^{{}^{\prime }}={\mathrm{F}}^{-1}(\mathcal{T})$，其中${\mathrm{F}}^{-1}$ 是$\mathrm{F}$的反函数。将$\mathcal{T}$映射到$\mathcal{S}$。

重建损失:${\ell }_{\mathrm{recon}}$用以衡量${\mathcal{S}}^{{}^{\prime }}$重建回$\mathcal{S}$之间的误差。而感知损失:${\ell }_{\mathrm{per}}$则用以维护${\mathcal{S}}^{{}^{\prime }}$和$\mathcal{S}$以及$\mathcal{T}$和${\mathcal{T}}^{{}^{\prime }}$之间的语义一致性。

【自监督学习/SSL】

        在F->M方向上，如果标签对于源域和目标域都涵盖（监督学习），那么计算其损失并最小化就可以得到一个比较理想的模型，但是在域自适应领域中，目标域的标签是不具备的。因此我们引入自监督学习方法（已经在半监督领域得到应用）进一步增强模型M的性能。其具体做法如下：

在经过一定批次的训练后，我们会获得源域$\mathcal{T}$的预测概率，在这些预测上我们可以得到一些伪标签${\hat{Y}}_{\mathcal{T}}$。（设置阈值，剔除低置信度的结果），在我们拿到这些伪标签后就可以直接将它们送入分割网络中进行学习。以进一步对齐它们之间的损失。于是将学习M的总损失改写成如下形式：

$\begin{array}{rl}{\mathcal{L}}_{\mathrm{M}}& ={\lambda }_{\mathrm{adv}}{\ell }_{\mathrm{adv}}(\mathrm{M}({\mathcal{S}}^{{}^{\prime }}),\mathrm{M}(\mathcal{T}))\\ & +{\ell }_{\mathrm{seg}}(M({\mathcal{S}}^{{}^{\prime }}),Y_{\mathcal{S}})+{\ell }_{\mathrm{seg}}(\mathrm{M}({\mathcal{T}}_{\mathrm{ssl}}),{\hat{Y}}_{\mathcal{T}})\end{array}$

其中${\mathcal{T}}_{\mathrm{ssl}}$是$\mathcal{T}$的子集，它拥有一部分伪标签:${\hat{Y}}_{\mathcal{T}}$.它一开始可以是空集。当达到更好的分割适应模型M时，我们可以用M来为T预测更高置信度的标签，导致${\mathcal{T}}_{\mathrm{ssl}}$的大小增长。我们使用的SSL与对抗学习相结合，可以更好地适用于分段自适应模型。直观地理解这个过程可以看下图：

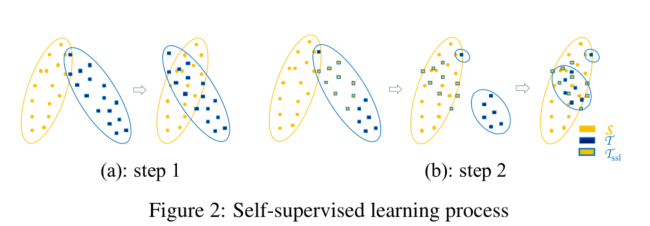
大体意思就是，第一步我们利用传统的域自适应模型已经对齐了一部分图像特征，从第二部分我们将已经对齐得不错的图像特征剔除，再进一步利用伪标签将剩下未对齐部分的特征对齐到源域上。其算法步骤如下：

【网络架构和损失函数】

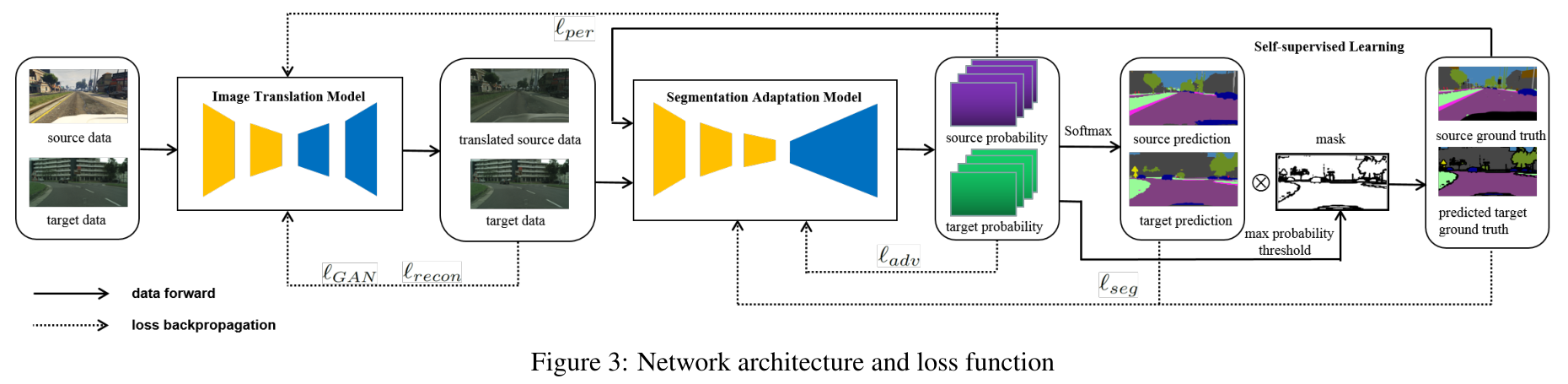
如图所示，整个网络框架由两部分组成：图像翻译模块，域自适应分割模块。

        在训练图像翻译模块过后，${\ell }_{\mathrm{GAN}}$和${\ell }_{\mathrm{recon}}$就可以定义为：

${\ell }_{\mathrm{GAN}}({\mathcal{S}}^{{}^{\prime }},\mathcal{T})={\mathbb{E}}_{I_{\mathcal{T}}\sim \mathcal{T}}[D_{\mathrm{F}}(I_{\mathcal{T}})]$

${\ell }_{\mathrm{recon}}(\mathcal{S},{\mathrm{F}}^{-1}({\mathcal{S}}^{{}^{\prime }}))={\mathbb{E}}_{I_{\mathcal{S}}\sim \mathcal{S}}[||{\mathrm{F}}^{-1}((I_{{\mathcal{S}}^{{}^{\prime }}}))-I_{\mathcal{S}}||]$

其中$I_{\mathcal{S}}$和$I_{\mathcal{T}}$是来自源数据集和目标数据集的输入图像。$I_{{\mathcal{S}}^{{}^{\prime }}}$是F给出的翻译图像，添加鉴别器$D_{\mathrm{F}}$是为了减小$I_{\mathcal{T}}$和$I_{\mathcal{S}}^{{}^{\prime }}$之间的差异而加入的鉴别器，对于重建损失，用L1范数保持$I_{\mathcal{S}}$和${\mathrm{F}}^{-1}(I_{\mathcal{S}}^{{}^{\prime }})$的一致性。

        如图3所示，感知损失联系了翻译模型和分段适应模型。当我们学习翻译模型的感知损失时，我们不是只保持$I_{\mathcal{S}}$和它的翻译结果$I_{\mathcal{S}}^{{}^{\prime }}$之间的语义一致性，而是每次重构增加一个用$\lambda$加权的项，以保持$I_{\mathcal{S}}$和它相应的重构${\mathrm{F}}^{-1}(I_{\mathcal{S}}^{{}^{\prime }})$之间的语义一致性。有了新的感知，翻译模型可以更加稳定，尤其是对于重建部分。${\ell }_{\mathrm{per}}$定义为:

$\begin{array}{rl}{\ell }_{\mathrm{per}}(\mathrm{M}(\mathcal{S}),\mathrm{M}({\mathcal{S}}^{{}^{\prime }}))& ={\lambda }_{\mathrm{per}}{\mathbb{E}}_{I_{\mathcal{S}}\sim \mathcal{S}}||\mathrm{M}(I_{\mathcal{S}})–\mathrm{M}((I_{\mathcal{S}}^{{}^{\prime }}))|{|}_1\\ & +{\lambda }_{\mathrm{per}\mathrm{\_}\mathrm{recon}}{\mathbb{E}}_{I_{\mathcal{S}}\sim \mathcal{S}}[||\mathrm{M}({\mathrm{F}}^{-1}((I_{\mathcal{S}}^{{}^{\prime }})))–\mathrm{M}(I_{\mathcal{S}})|{|}_1]\end{array}$

        同理${\ell }_{\mathrm{per}}(M(\mathcal{T}),\mathrm{M}({\mathcal{T}}^{{}^{\prime }}))$定义类似。

在分段自适应模型训练，需要带有损失的对抗性学习和带有损失的自我监督学习。对于对抗性学习，我们添加了一个鉴别器来减少上图所示的源概率和目标概率之间的差异。${\ell }_{\mathrm{adv}}$可以定义为:

${\ell }_{\mathrm{adv}}(M({\mathcal{S}}^{{}^{\prime }}),\mathrm{M}(\mathcal{T}))={\mathbb{E}}_{I_{\mathcal{T}}\sim \mathcal{T}}[D_{\mathrm{M}}(M(I_{\mathcal{T}}))]$

分割损失直接应用交叉熵损失，源域的分割损失定义如下：

$\begin{array}{r}{\ell }_{\mathrm{seg}}(M({\mathcal{S}}^{{}^{\prime }}),Y_{\mathcal{S}})=-\frac{1}{HW}\sum _{H,W}\sum _{c=1}^C{\mathbb{l}}_{[c=y_s^{hw}]}\log P_{\mathcal{S}}^{pwc}\end{array}$

        于目标域图像$I_{\mathcal{T}}$，我们需要定义如何为其选择伪标签映射${\hat{y}}_{\mathcal{T}}$。我们选择使用一种称之为“max probability thresholdMPT)”的常用方法来过滤像素中具有高预测置信度的像素。因此，我们可以定义${\hat{y}}_{\mathcal{T}}$ ,其中 ${\hat{y}}_{\mathcal{T}}=\arg max\mathrm{M}(I_{\mathcal{T}})$和${\hat{y}}_{\mathcal{T}}$作为 $m_{\mathcal{T}}={\mathbb{l}}_{[\arg max\mathrm{M}(I_{\mathcal{T}})>\mathrm{threshold}]}$的掩码映射。因此，它的分割损失可以表示为:

$\begin{array}{r}{\ell }_{\mathrm{seg}}(\mathrm{M}({\mathcal{T}}_{\mathrm{ssl}}),{\hat{Y}}_{\mathcal{T}})=-\frac{1}{HW}\sum _{H,W}{m}_{\mathcal{T}}^{hw}\sum _{c=1}^c{\mathbb{l}}_{[c=y_{\mathcal{T}}^{hw}]}\log P_{\mathcal{T}}^{hwc}\end{array}$

【总结】

        这篇文章的思路很有意思，双向学习思路也很新颖，值得细品。

【参考文献】

• Yunsheng Li, Lu Yuan,Nuno Vasconcelos.Bidirectional Learning for Domain Adaptation of Semantic Segmentation.in CVPR 2019