【CapsNet】Dynamic Routing Between Capsules

【Backgroud】

这是一篇Hinton 大神与2017年发表于NIPS的文章，Arxiv传送点。

更深刻理解胶囊网络传送点。

【Rethinking in a set of picture】

引用前人总结的一个例子：

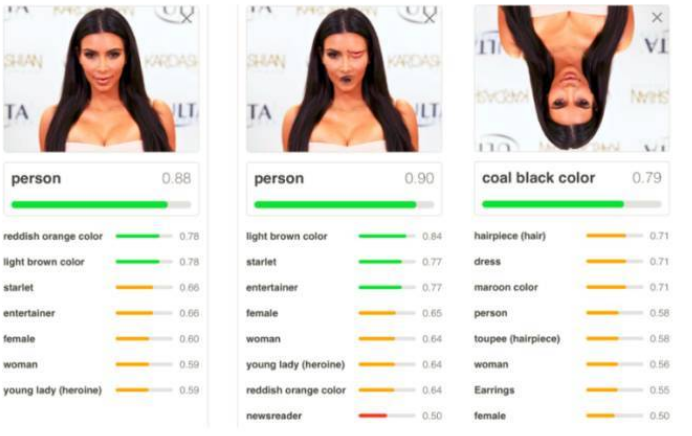
从图中我们知道当前流行的CNN的一些缺陷。：

第一张 CNN 给出的答案是人，概率为 0.88，正确；第二张 CNN 给出的答案也是人，概率为 0.90 ，开玩笑在？第三张 CNN 给出的答案是黑发，概率为 0.79 ，和悠悠一样天真。

CNN 弄错的两张图也是因为它的两个缺陷：

1、CNN 对物体之间的空间关系 (spatial relationship) 的识别能力不强，比如嘴巴和眼睛换位置了还被识别成人？

2、CNN 对物体旋转之后的识别能力不强 (微微旋转还可以)，比如人倒过来就被识别成头发了？

【Convolutional neural networks are doomed】

    现阶段要解决现阶段CNN展示出的问题，众多科研工作者仍不断地尝试，为联系CNN与图像空间关系，现阶段的工作重心开始往Learning + Reasoning 发展, 而为解决识别的鲁棒性，有的工作则从数据集下手，通过数据增强等技术进行改善。但带来的是计算力的需求日益增加。

    Hinton 如此说道："卷积神经网络要完蛋了”，因此他前不久也提出了一个 Capsule 的东西，直译成胶囊。但是这个翻译丢失了很多重要的东西，个人认为叫做向量神经元 (vector neuron) 甚至张量神经元 (tensor neuron) 更贴切。

【Prerequisite】

    要入门CapsNet需理解其背后的原理，本章从一些先修知识出发，浅要介绍一些CapsNet相对于CNN进行的Reasoning知识。

Pose:

    In order to correctly do classification and object recognition, it is important to preserve hierarchical pose relationships between object parts. 

— Hinton

    为了正确的分类和识别物体，保持物体部分之间的分层姿态 (hierarchical pose) 关系是很重要的。姿态主要包括平移 (translation)、旋转 (rotation) 和放缩 (scale) 三种形式。

    在拍摄人物时，我们调动照相机的角度从 3D 的人生成 2D 的照片。照出来的人物照角度多种多样，但人是个整体 (脸和身体对于人的相对位置不会变)。因此我们不想定义相对于相机的所有对象 (脸和身体)，而将它们定义一个相对稳定的坐标系 (coordinate frame) 中，然后仅仅通过转动相机来照出不同角度的照片。

    Hinton 认为，为了正确地进行分类和对象识别，重要的是保持对象部分之间的分层姿态关系。后面讲到的 Capsule 就符合这个重要直觉，它结合了对象之间的相对关系，并以姿态矩阵来表示。

Post matrix:

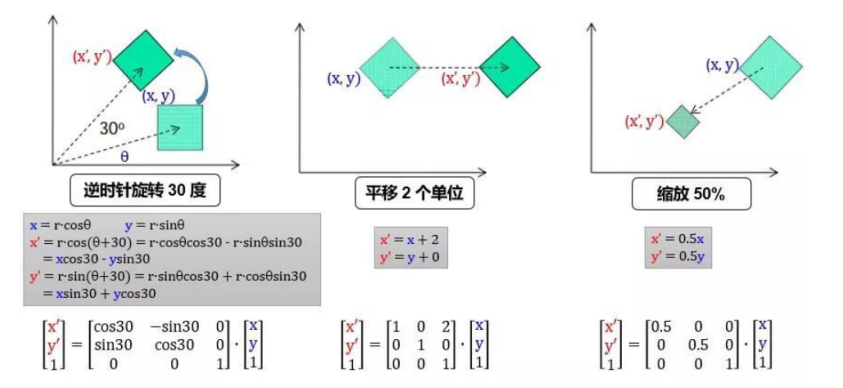
    在创建这些图形时，我们首先会定义脸和身体相对于人的位置，更进一层，我们会定义眼睛和嘴巴对于相对于脸的位置，但不是相对于人的位置。因为之前已经有了脸相对于人的位置，现在又有了眼睛相对于脸的位置，那么也有了眼睛相对于人的位置。本质上，你将有层次的创建一个完整的人，而所需要的数学工具就是姿态矩阵 (pose matrix)，这个矩阵定义所有对象相对于照相机的视点 (viewpoint)，并且还表示了部件与整体之间的关系。

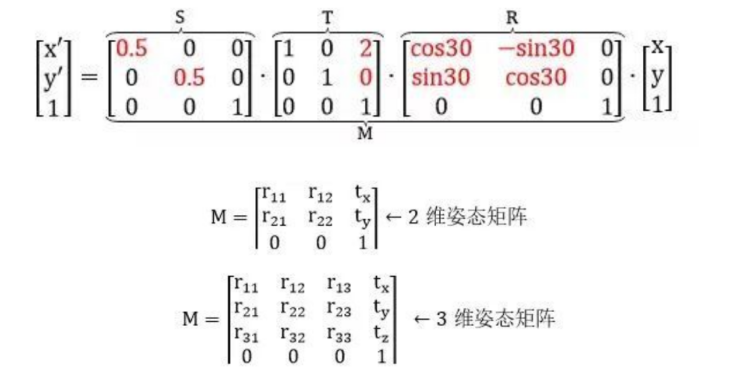
    用 R, T, S 定义旋转、平移和缩放矩阵，那么将 (x, y) 先逆时针转 30 度，再向右平移 2 个单位，最后缩放 50% 到 (x', y') 可以由下列矩阵连乘得到

    在 2 维平面中，我们加了 1 个维度 z，是为了方便完成平移操作。写出 2 维平面姿态矩阵 M 的一般形式，并延伸并类比到 3 维空间的姿态矩阵，表示如下：

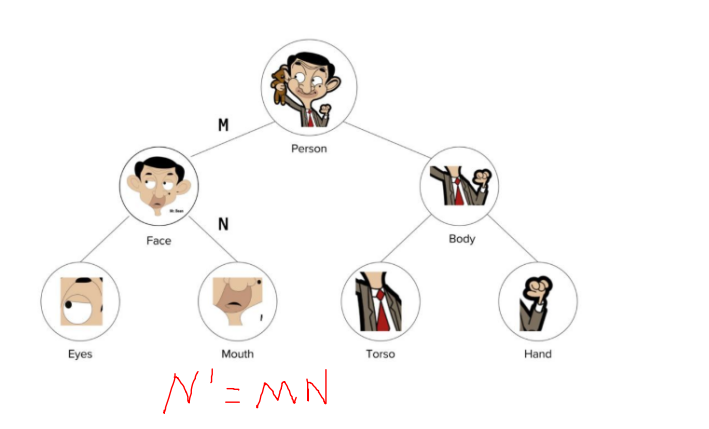
整体是由它的各个部分组成的，如上图：

人 (整体) 是由脸和身体组成

脸 (整体) 是由眼睛和嘴巴组成

身体 (整体) 是由躯干和手组成

每个部分通过一个姿态矩阵与其主体相关联。如果 M 是脸对人姿态矩阵，N 是嘴巴对脸姿态矩阵，那么嘴巴对人的姿态矩阵为 \(N' = MN\)

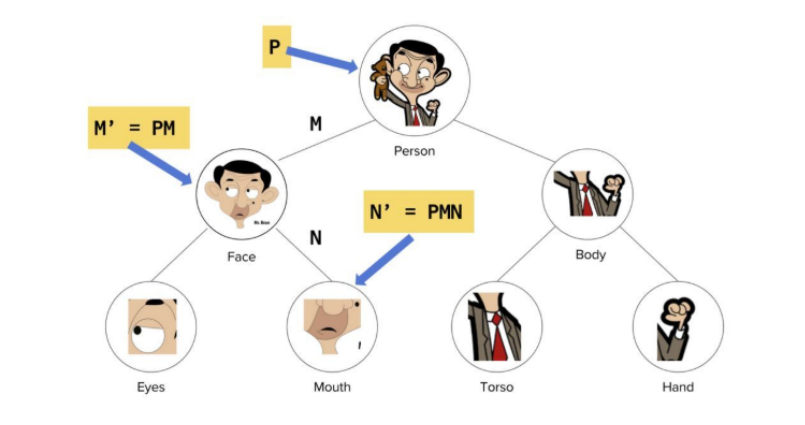
    现在我们有一个照相机，并且我们知道人对相机的帧的姿态矩阵是 P，可以通过连乘姿态矩阵来提取人的每个部分的所有基本属性，比如：

脸对相机的帧的姿态矩阵由 \(M' = PM \) 给出

嘴对相机的帧的姿态矩阵由 \(N' = M'N = PMN\) 给出

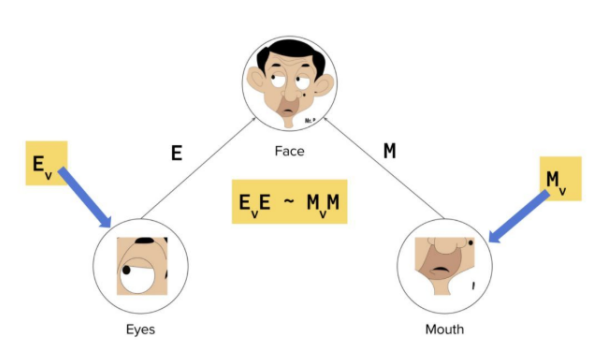
    现在告诉你左眼的位置，你可以想象脸的位置了吧。同理，你以为可以从嘴的位置估计脸的位置。如果由左眼和嘴的位置推出脸的位置相符，数学上表示为 \(E_v \cdot E = M_v \cdot M\)，其中

\( E_v \) 是眼睛的位置向量

\(E \)是眼睛对脸的姿态矩阵

\(M_v\) 是嘴巴的位置向量

\(M\)是嘴巴对脸的姿态矩阵

还记得引言中正常的人脸的图像 (左图) 吗？从嘴和左眼推出脸的位置是相似的，因此得出结论它们属于同一个脸。

但是对于非正常的人脸的图像 

从嘴位置推出脸在图像上角 

从左眼位置推出脸在图像底部 

从嘴和左眼的位置出发得到的结论似乎不相符 (disagreement)，因此它们不应该被认为出现在同一张脸上。只有当嘴和左眼处在正确的位置，从它们出发得到的结论才会相符 (agreement)。在这种情况下，我们就会发现嘴巴应该在两只眼睛的下面的中间，只有这样放置的眼睛和嘴巴才是脸部的一部分，而不是仅仅靠一张嘴巴和眼睛来识别脸部。

不变形与同变性

• The invariance of the broad sense, (invariance) is said (representation) does not change with transform (transformation); 

• Equivariance is the representation of the transformation equivalent to the representation of the transform bation.

    广义上讲，不变性 (invariance) 是表示 (representation) 不随变换 (transformation) 变化；而同变性(equivariance) 是表示的变换等价于变换的表示。

    从计算机视觉角度上讲，不变性指不随一些变换来识别一个物体，具体变换包括平移 (translation)，旋转 (rotation)，视角 (viewpoint)，放缩 (scale) 等，如下图所示：

    不变性通常在物体识别上是好事，因为不管雕像怎么平移、2D旋转、3D旋转和放缩，我们都可以识别出它是雕像。

如果我们的任务比物体识别稍微困难一点，比如我想知道雕像平移了多少个单位，旋转了多少度，放缩了百分之多少，那么不变性远远不够，这时需要的是同变性。

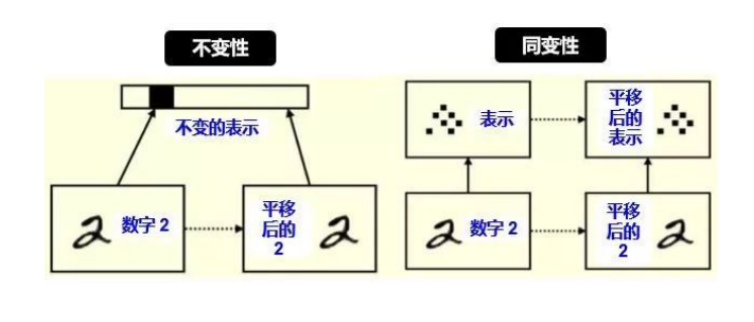
对平移和旋转的不变性，其实是丢弃了“坐标框架”，而同变性不会丢失这些信息，它只是对内容的一种变换。具体来讲：

左图：平移前的 2 和平移后的 2 的表示是一样的 (比如用 CNN 的池化)，这样我们只能识别出 2 ，根本无法判断出 2 在图像中的位置。

右图：平移前的 2 和平移后的 2 的表示里含有位置这个信息 (比如用 Capsule)，这样我们不但能识别出 2，还能判断出 2 在图像中的位置。

【Rethinking In Pooling】

    The pooling operation used in convolutional neural networks is a big mistake and the fact that it works so well is a disaster. 

— Hinton

    Hinton 认为池化在 CNN 的好效果是个大错误甚至灾难。因为池化会导致重要的信息丢失，如果它是两层之间的信使，它告诉第二层的是“我们看到左上角有一个最大值 2，右上角有一个最大值 4”，但不知道这个 2 和 4 是从第一层哪里来的。在引言的例子中，我们知道“两只眼睛一个鼻子一张嘴巴”并不代表“一张脸”，要确认是张脸，我们还需要知道这些器官之间的相互位置，比如眼睛要在鼻子上方，鼻子要在嘴巴上方，那么才可能是张脸。

【What is the Capsule?】

• A vehicle that contains multiple neurons which represent various properties of a particular entity that appears in an image

• These properties contain multiple types of instantiation parameter (eg. Pose, Transformation, Speed, Color, texture)

• Its output value is the probability of the entity's existence.

    胶囊 (Capsule) 是一个包含多个神经元的载体，每个神经元表示了图像中出现的特定实体的各种属性。这些属性可以包括许多不同类型的实例化参数 (instantiation parameter)，例如姿态 (位置、大小、方向)，变形，速度，色相，纹理等。胶囊里一个非常特殊的属性是图像中某个类别的实例的存在。它的输出数值大小就是实体存在的概率。

【Compare with vetor】

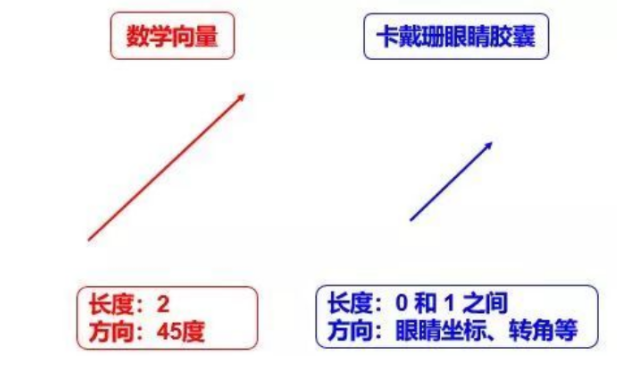
    数学上常说的向量是一个有方向和长度的概念，把胶囊类比于数学向量，它也有所谓的“长度”和“方向”。假设一个胶囊代表人脸的眼睛，戏称“人脸眼睛胶囊”，那么其

长度代表眼睛在图像某个位置存在的概率

方向代表眼睛的一些参数，比如位置，转角，清晰度等等

【Capsule vs scalar neuron】

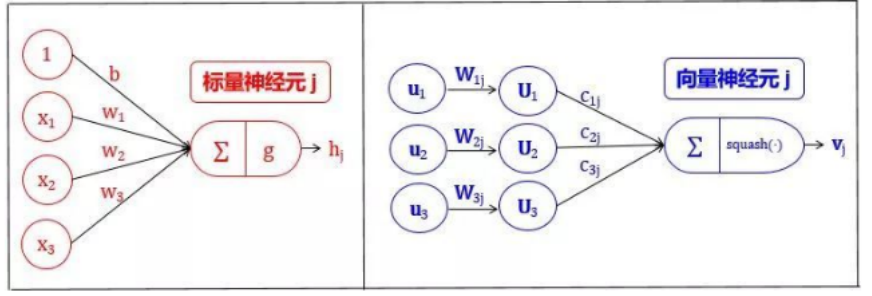
    我们将 Capsule 称作向量神经元 (vector neuron, VN)，而普通的人工神经元叫做标量神经元 (scalar neuron, SN)

SN 从其他神经元接收输入标量，然后乘以标量权重再求和，然后将这个总和传递给某个非线性激活函数 (比如 sigmoid, tanh, Relu)，生出一个输出标量。该标量将作为下一层的输入变量。实质上，SN 可以用以下三个步骤来描述：

将输入标量 \(x\) 乘上权重 \(w\)

对加权的输入标量求和成标量 \(a\)

用非线性函数将标量 \(a\)转化成标量\(h\)

VN的步骤在 SN的三个步骤前加一步：

将输入向量 \(u\) 用矩阵 \(W\)加工成新的输入向量\(U\)

将输入向量 \(U\)乘上权重 \(c\)

对加权的输入向量求和成向量 \(s\)

用非线性函数将向量 \(s\)转化成向量 \(v\)

【Step 1: Matrix transormation】

上一层的 VN代表眼睛 (\(u_1\)), 鼻子 (\(u_2\)) 和嘴巴 (\(u_3\))，称为低层特征

下一层第 j 个的VN代表脸，称为高层特征。注意下一层可能还有很多别的高层特征，脸是最直观的一个

\(U_{j|1}\)是根据眼睛位置来检测脸的位置

\(U_{j|2}\)是根据鼻子位置来检测脸的位置

\(U_{j|3}\)是根据嘴巴位置来检测脸的位置

    现在，直觉应该是这样的：如果这三个低层特征 (眼睛，鼻子和嘴) 的预测指向相同的脸的位置和状态，那么出现在那个地方的必定是一张脸。如图所示：

左图预测出脸，因为红蓝黄绿圈非常吻合；而右图没有没有预测出脸，因为红蓝黄绿圈相差甚远。

【Step 2: Input weighted】

\( C_{ij} \times U_{j|i}\)

    这个步骤和标量神经元SN的加权形式有点类似。在 SN的情况下，这些权重是通过反向传播 (backward propagation) 确定的，但是在 VN的情况下，这些权重是使用动态路由 (dynamic routing) 确定的, 如果从高层面来解释动态路由，如图：

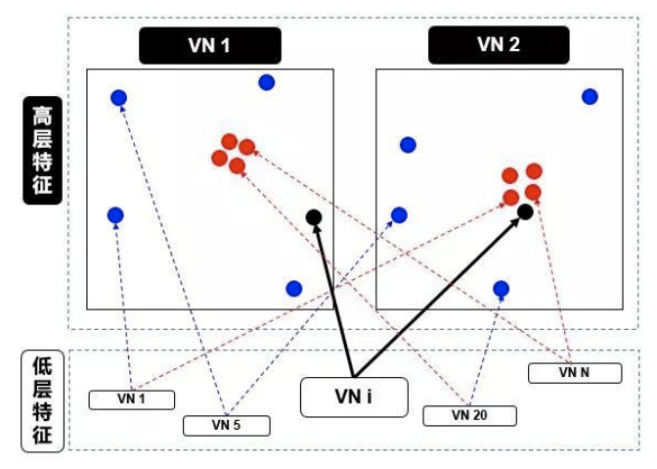
    在上图中，我们有一个较低级别 \(VN_i\)需要“决定”它将发送输出给哪个更高级别 \(VN_1\)和 \(VN_2\)。它通过调整权重 \(c_{i1}\)和\(C_{i2}\)来做出决定。

现在，高级别 \(VN_1\)和 \(VN_2\)已经接收到来自其他低级别 VN 的许多输入向量，所有这些输入都以红点和蓝点表示。

红点聚集在一起，意味着低级别 VN 的预测彼此接近

蓝点聚集在一起，意味着低级别 VN 的预测相差很远

那么，低别级 \(VN_i\)应该输出到高级别 \(VN_1\)还是 \(VN_2\)？这个问题的答案就是动态路由的本质。由图看出

\(VN_i\)的输出远离高级别 \(VN_1\)中的“正确”预测的红色簇

\(VN_i\)的输出靠近高级别 \(VN_2\) 中的“正确”预测的红色簇

而动态路由会根据以上结果产生一种机制，来自动调整其权重，即调高 \(VN_2\)相对的权重 \(c_{i2}\)，而调低 \(VN_1\)相对的权重 \(c_{i1}\)。

【Step 3: Sum weighted】

\(\begin{align}S_j = \sum_{i} C_{ij} U_{j|i} \end{align}\)

    这一步类似于普通的神经元的加权求和步骤，除了总和是向量而不是标量。加权求和的真正含义就是计算出第二步里面讲的红色簇心 (cluster centroid)。

【Step 4: Nonlinear-activation: Squash function】

\( V_i = \frac{||s_j||}{1+||s_j||^2} \cdot \frac{s_j}{||s_j||}\)

    这个函数主要功能是使得 \(v_j\) 的长度不超过 1，而且保持 \(v_j\)和 \(s_j\)同方向。

公式第一项压扁函数

    如果 \(s_j\) 很长，第一项约等于 1

    如果 \(s_j\)很短，第一项约等于 0

公式第二项单位化向量 \(s_j\)，因此第二项长度为 1

这样一来，输出向量 \(v_j\)的长度是在 0 和 1 之间的一个数，因此该长度可以解释为 VN 具有给定特征的概率。

【Step 5: Dynamic Routing】

    刚刚讲过，低级别 VNi 需要决定如何将其输出向量发送到高级别 VNj，它是通过改变权重 cij而实现的。首先来看看 cij的性质：

每个权重是一个非负值

•     对于每个低级别 VNi，所有权重 cij 的总和等于 1

•     对于每个低级别 VNi，权重的个数等于高级别 VN 的数量

    权重由迭代动态路由 (iterative dynamic routing) 算法确定

    前两个性质说明 c 符合概率概念。回想一下刚刚讲的，VN 的长度被解释为它的存在概率。VN 的方向是其特征的参数化状态。因此，对于每个低级别 \(VN_i\)，其权重 \(c_{ij}\)定义了属于每个高级别 \(VN_j\)的输出的概率分布。

    低级别 VN 会将其输出发送到“同意”该输出的某个高级别 VN。这是动态路由算法的本质。

第 1 行：这个过程用到的所有输入 – l 层的输出 \(U_{j|i}\)，路由迭代次数 r

第 2 行：定义 \(b_{ij}\)是 l 层 \(VN_i\) 应该连接 l+1 层 \(VN_j\)的可能性，初始值为 0

第 3 行：执行第 4-7 行 r 次

第 4 行：对 l 层的 \(VN_i\)，将 \(b_{ij}\) 用 softmax 转化成概率 \(c_{ij}\)

第 5 行：对 l+1 层的 \(VN_j\)，加权求和 \(s_j\)

第 6 行：对 l+1 层的 \(VN_j\)，压缩 \(s_j\) 得到 \(V_j\)

第 7 行：根据 \(U_{j|i}\) 和\(v_j\)的关系来更新 \(b_{ij}\)

第 1 行无需说明，唯一要指出的是迭代次数为 3 次，Hinton 在他论文里这样说道

第 2 行初始化所有 b 为零，这是合理的。因为从第 4 行可看出，只有这样 c 才是均匀分布的，暗指“l 层 VN 到底要传送输出到 l+1 层哪个 VN 是最不确定的”

第 4 行的 softmax 函数产出是非负数而且总和为 1，致使 c 是一组概率变量

第 5 行的 \(s_j\)就是小节 2.3 第二步里面讲的红色簇心，可以认为是低层所有 VN 的“共识”输出

第 6 行的 squash 确保向量 \(s_j\) 的方向不变，但长度不超过 1，因为长度代表 VN 具有给定特征的概率

第 7 行是动态路由的精华，用 \(U_{j|i}\)和 vj 的点积 (dot product) 更新 \(b_{ij}\)，其中前者是 l 层 \(VN_i\)对 l+1 层 \(VN_j\)的“个人”预测，而后者是所有 l 层 VN 对 l+1 层 \(VN_j\) 的“共识”预测：

当两者相似，点积就大，\(b_{ij}\)就变大，低层 \(VN_i\)连接高层 \(VN_j\) 的可能性就变大

当两者相异，点积就小，\(b_{ij}\)就变小，低层 \(VN_i\)连接高层 \(VN_j\)的可能性就变小

下面两幅图帮助进一步理解第 7 行的含义，第一幅讲的是点积，论文中用点积来度量两个向量的相似性，当然还有很多别的度量方式。

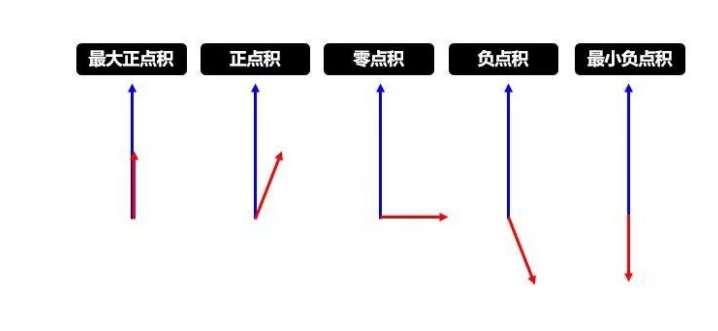
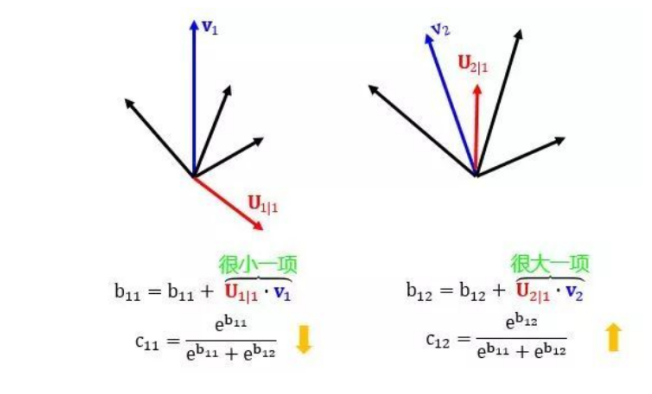
更新权重，此消彼长。

【Architecture】

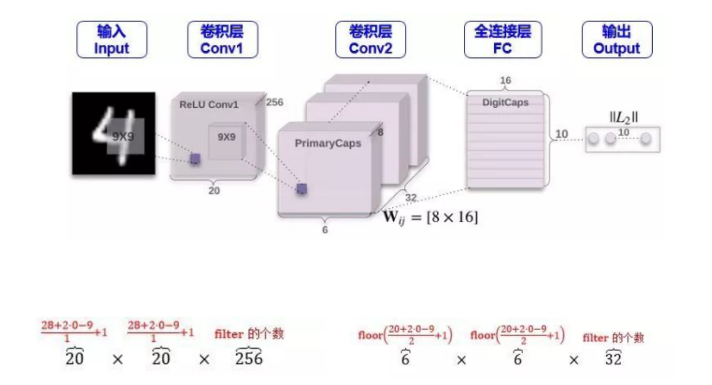
CONV1

    这一步就是一个常规的卷积操作，用了 256 个 stride 为 1 的 9×9 的 filter，得到一个 20x20x256 的输出。按照原文的意思，这一步主要作用就是对图像像素做一次局部特征检测。让我们 Conv1 层的维度是如何得到的。(但为什么不一开始就用 Capsule 呢？因为 Capsule 是用来表征某个物体的“实例”，因此它更适合于表征高级的实例。如果直接用 Capsule 吸取图片的低级特征内容，不是很理想，而 CNN 却擅长抽取低级特征，因此一开始用 CNN 是合理的)

CONV2(低级特征到 Primary Capsule)

    Conv2 层才是开始含有 Capsule。如果按照普通 CNN 里面的做法，用了 32 个 stride 为 2 的 9x9x256 的 filter，也只能得到 6x6x32 的输出，算法如下：

    但是从上图和 Hinton 的论文发现，Conv2 层的维度是 6x6x8x32。这个 8怎么来的？它又代表着什么含义？个人理解是用 32 个 stride 为 2 的 9x9x256 的filter做了 8次卷积操作，而且

•     在 CNN 中，维度为 6x6x1x32 的层里有 6x6x32 元素，每个元素是一个标量

•     在 Capsule 中，维度为 6x6x8x32 的层里有 6x6x32 元素，每个元素是一个 1×8的向量，既 capsule

Conv2 层的输出在论文中称为 Primary Capsule，简称 PrimaryCaps，主要储存低级别特征的向量。

Primary Capsule 到 Digit Capsule (FC)

    下一层就是存储高级别特征的向量，在本例中就是数字，FC 层的输出在论文中称为 Digit Capsule，简称 DigitCaps。PrimaryCaps 和 DigitCaps 是全连接的，但不是像传统神经网络标量和标量相连，而是向量与向量相连。

    PrimaryCaps 里面有 6x6x32 元素，每个元素是一个 1×8的向量，而 DigitCaps 有 10 个元素 (因为有 10 个数字)，每个元素是一个 1×16的向量。为了让 1×8向量与 1×16向量全连接，需要 6x6x32 个 8×16的矩阵 (姿态矩阵还记得吗)。

    现在 PrimaryCaps 有 6x6x32 = 1152 个 VN，而 DigitCaps 有 10 个 VN，那么 I = 1,2, …, 1152, j = 0,1, …, 9。再用小节 2.4 讲的动态路由算法迭代 3 次计算 \(c_{ij}\)并输出 10 个 \(v_j\)。

Digit Capsule 到最终输出

    根据 Capsule 定义，它的长度表示其表征的内容出现的概率，所以做分类时取输出向量的 L2 范数 (也就是长度) 即可。需要注意的是，最后 Capsule 输出的概率总和并不等于 1，也就是 Capsule 有同时识别多个物体的能力。

损失函数

\( L_k = T_k \max (0, m^+ – ||V_k||)^2 + \lambda (1-T_k) \max(0, ||V_k|| – m^-)^2\)

下标\(k\)是分类

\( T_k \)是分类的指示函数 (k 类存在为 1，不存在为 0)

\( m^+\)为上界，惩罚假阳性 (false positive) ，即预测 k 类存在但真实不存在，识别出来但错了

\( m^-\)为下界，惩罚假阴性 (false negative) ，即预测 k 类不存在但真实存在，没识别出来

\( \lambda\)是比例系数，调整两者比重

总的损失是各个样例损失之和。论文中 \( m^+ = 0.9, m^- = 0.1, \lambda = 0.5\)，用大白话说就是

如果 k 类存在，\( ||V_k||\)不会小于 0.9

如果 k 类不存在，\( ||V_k||\) 不会大于 0.1

惩罚假阳性的重要性大概是惩罚假阴性的重要性的 2 倍

【Something Next To Do】

• How to improve the performance of CapsNet (not the most important)

• Do the method “Learning plus(Learning + Inference)” will be the next generation of Deep learning technology? (important)

• What can I do for Semantic Segmentation by fusing these method(not only CapsNet, but also GNN etc.) proposed by forerunner? (most important)

【References】

• Sabour S, Frosst N, Hinton G E. Dynamic Routing Between Capsules[J]. NIPS2017

• 王圣元.看完这篇别说你还不懂胶囊网络.王的机器(公众号)